题目内容
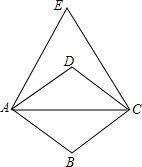如图，四边形ABCD是菱形，以对角线AC为边向上作等边△ACE．已知∠DAB=70°，则∠EAD的大小为（ ）| A、25° | B、35° |
| C、45° | D、55° |
考点：菱形的性质
专题：
分析：根据菱形的性质求出∠DAC，根据等边三角形的性质求出∠EAC，即可求出答案．
解答：解：∵四边形ABCD是菱形，
∴∠DAC=
∠DAB，
∵∠DAB=70°，
∴○DAC=35°，
∵△ACE是等边三角形，
∴∠EAC=60°，
∴∠EAD=60°-35°=25°，
故选A．
∴∠DAC=
| 1 |
| 2 |
∵∠DAB=70°，
∴○DAC=35°，
∵△ACE是等边三角形，
∴∠EAC=60°，
∴∠EAD=60°-35°=25°，
故选A．
点评：本题考查了菱形的性质，等边三角形的性质的应用，注意：菱形的对角线平分一组对角，难度适中．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
一个函数具有下列性质：①它的图象经过点（-1，1）；②它的图象在二、四象限内；③在每个象限内，函数值y随自变量x的增大而增大．则这个函数的解析式可以为（ ）
| A、y=-x+1 | ||
B、y=
| ||
| C、y=-x2 | ||
D、y=-
|
如图，在Rt△ABC中，∠C=90°，∠B=30°，AC=6，解这个直角三角形．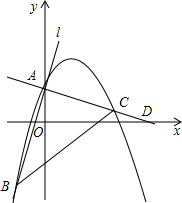
如图，抛物线y=ax2+bx+2与直线l交于点A、B两点，且A点为抛物线与y轴的交点，B（-2，-4），抛物线的对称轴是直线x=2，过点A作AC⊥AB，交抛物线于点C、x轴于点D．已知圆的半径是R，则圆内接正十边形的边长是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
“三月三，放风筝”，这天，妈妈让小玉自己动手制作一个如图所示的小风筝，它由两个三角形拼成，而且要满足△ABC≌△ADE才符合要求，小玉通过测量得到AB=AD，∠BAE=∠DAC，为了保证符合要求，还需要测量哪一对相等的量？请你帮助小玉找出一对相等的量并说明理由．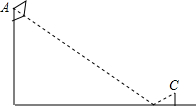
为测量学校操场上旗杆的高度，某数学活动小组设计如下测量方法：将镜子放在离旗杆（AB）27m的点E处，然后沿直线BE后退，使在点D处恰好看到旗杆顶端A在镜子中的像与镜子上的标记重合（如图），若DE=2.4m，观测者的眼睛离地面的高度CD为1.6m，求旗杆的高度．
已知二次函数的图象（0≤x≤3）如图所示，关于函数在所给变量取值范围内，函数y最小值=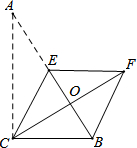
如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=3，点E是AB的中点．将△ACE沿CE折叠后得到△CEF，点A落在F点处，CF交AB于点O，连结BF，则四边形BCEF的面积是