题目内容
2.若x=$\sqrt{29}$-3,则$\sqrt{{x}^{2}+6x+5}$的值为5.分析 先把x=$\sqrt{29}$-3变形得到x+3=$\sqrt{29}$,由x2+6x+5=(x+3)2-4,然后整体代入进行计算.
解答 解:∵x=$\sqrt{29}$-3,
∴x+3=$\sqrt{29}$,
∴$\sqrt{{x}^{2}+6x+5}$=$\sqrt{(x+3)^{2}-4}$=5.
故答案为:5.
点评 本题考查了二次根式的化简求值,利用完全平方公式变形所求的代数式,再运用整体代入的方法求代数式的值

练习册系列答案
相关题目
17.已知a<0,那么$\sqrt{(a-1{)^2}}+\sqrt{a^2}$可化简为( )
| A. | 2a-1 | B. | 1-2a | C. | -1 | D. | 1 |
14. 已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
 已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )| A. | 18° | B. | 30° | C. | 36° | D. | 72° |
11.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{1}{2}({x^2}+1)$,$\frac{3xy}{π}$,$\frac{3}{x+y}$中,分式的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.把cos12°、sin21°、cos67°、sin69°排列大小正确的是( )
| A. | cos12°<sin21°<cos67°<sin69° | B. | sin21°<cos12°<cos67°<sin69° | ||
| C. | sin21°<cos67°<sin69°<cos12° | D. | cos67°<cos12°<sin21°<sin69° |
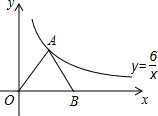 如图,点A在双曲线y=$\frac{6}{x}$上,B为x轴正半轴上一点,连结OA、AB且AO=AB,则△AOB的面积是6.
如图,点A在双曲线y=$\frac{6}{x}$上,B为x轴正半轴上一点,连结OA、AB且AO=AB,则△AOB的面积是6.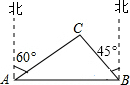 我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)