题目内容
2. 如图,抛物线y1=-x2+2x+3与直线y2=4x交于A,B两点.
如图,抛物线y1=-x2+2x+3与直线y2=4x交于A,B两点.(1)求A,B两点的坐标;
(2)当x取何值时,y1>y2?
分析 (1)联立两函数解析式求解即可;
(2)根据函数图象写出抛物线直线上方部分的x的取值范围即可.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}{{y}_{1}={-x}^{2}+2x+3}\\{{y}_{2}=4x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-12}\end{array}\right.$,
所以A点的坐标是(1,4),B点的坐标是(-3,-12);
(2)由图可知,-3<x<1时,y1>y2.
点评 本题考查了二次函数与不等式,主要利用了联立两函数解析式求交点坐标的方法,利用函数图象求不等式的解集,利用数形结合的思想求解是更简便.

练习册系列答案
相关题目
12.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a2+b2的值为( )
| A. | 36 | B. | 50 | C. | 28 | D. | 25 |
10.计算(-3)×2-1的结果是( )
| A. | -5 | B. | -7 | C. | 6 | D. | -6 |
9.若M(1-3x2)=1-9x4,则M等于( )
| A. | 1-3x2 | B. | (1-3x2)2 | C. | 1+3x2 | D. | (1+3x2)2 |
 如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大24°,则∠B′EA=68°.
如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大24°,则∠B′EA=68°.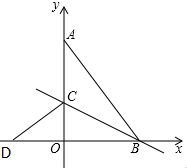 如图,在平面直角坐标系中,点A(0,8),B(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点D处,折痕所在的直线交y轴正半轴于点C,则直线DC的解析式为y=$\frac{3}{4}$x+3.
如图,在平面直角坐标系中,点A(0,8),B(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点D处,折痕所在的直线交y轴正半轴于点C,则直线DC的解析式为y=$\frac{3}{4}$x+3.