题目内容
5.解不等式组,并写出不等式组的正整数解.$\left\{\begin{array}{l}{\frac{x-1}{2}≤1}\\{x-2<4(x+1)}\end{array}\right.$.
分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后确定解集中的正整数解即可.
解答 解:$\left\{\begin{array}{l}{\frac{x-1}{2}≤1…①}\\{x-2<4(x+1)…②}\end{array}\right.$,
解①得:x≤3,
解②得:x>-2.
则不等式组的解集是:-2<x≤3.
则正整数解是1,2,3.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
相关题目
20.若-$\frac{a}{3}$≤-$\frac{a}{2}$,则a一定满足( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
12.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a2+b2的值为( )
| A. | 36 | B. | 50 | C. | 28 | D. | 25 |
 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}$x+6的图象分别交x、y轴于点A,B,与一次函数Y=kx的图象交于第一象限内的点C.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}$x+6的图象分别交x、y轴于点A,B,与一次函数Y=kx的图象交于第一象限内的点C.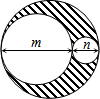 三圆位置如图,其中m、n分别是两个较小圆的直径,求图中阴影部分的面积.
三圆位置如图,其中m、n分别是两个较小圆的直径,求图中阴影部分的面积. 如图,在四边形ABCD中,对角线AC、BD互相垂直平分,若使四边形ABCD是正方形,则需要再添加的一个条件为AC=BD.(图形中不再添加辅助线,写出一个条件即可)
如图,在四边形ABCD中,对角线AC、BD互相垂直平分,若使四边形ABCD是正方形,则需要再添加的一个条件为AC=BD.(图形中不再添加辅助线,写出一个条件即可) 如图,∠AOB内部有两点M和N,请找出一点P,使得PM=PN,且点P到∠AOB两边的距离相等.(不写作图方法,保留作图痕迹)
如图,∠AOB内部有两点M和N,请找出一点P,使得PM=PN,且点P到∠AOB两边的距离相等.(不写作图方法,保留作图痕迹)