题目内容
5.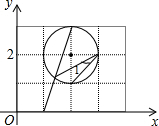 如图,sin∠1=$\frac{\sqrt{10}}{10}$.
如图,sin∠1=$\frac{\sqrt{10}}{10}$.
分析 先由圆周角定理:同弧所对的圆周角相等,可得∠1=∠A,然后在Rt△ABC中,由勾股定理可求AB的值,然后利用正弦的定义求出∠A的正弦即是∠1的正弦.
解答 解:如图所示,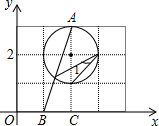
∵∠1=∠A,
∴sin∠1=sinA,
在Rt△ABC中,AC=3,BC=1,
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$,
∵sinA=$\frac{BC}{AB}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$,
∴sin∠1=$\frac{\sqrt{10}}{10}$,
故答案为:$\frac{\sqrt{10}}{10}$.
点评 本题考查的是圆周角定理,勾股定理,锐角三角函数的定义,熟知在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边是解答此题的关键.另外将∠1转化为∠A也是解题的关键.

练习册系列答案
相关题目
15.下列不等式解法正确的是( )
| A. | 如果-$\frac{1}{2}$x>2,那么x<-1 | B. | 如果-x>6,那么x<6 | ||
| C. | 如果2x<-2,那么x>-1 | D. | 如果$-\frac{1}{2}x<0$,那么x>0 |
16.(3a+2)(4a2-a-1)的结果中二次项系数是( )
| A. | -3 | B. | 8 | C. | 5 | D. | -5 |
10.若一个棱长均为a的三棱柱,它的主视图和俯视图分别是正方形和正三角形,则它的左视图的面积为( )
| A. | $\frac{\sqrt{3}}{2}$a2 | B. | $\frac{\sqrt{3}}{4}$a2 | C. | $\sqrt{3}$a2 | D. | a2 |
14. 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是( )
甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是( )
 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是( )
甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 不确定 |
15.在y=□x2□4x□4的□中,任意填上“+”或“-”,可组成若干个不同的二次函数,其中其图象与x轴只有一个交点的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |