题目内容
 如图,正方形ABCD和正方形BEFG平放在一起.
如图,正方形ABCD和正方形BEFG平放在一起.(1)若两正方形的面积分别是9和4,直接写出边AE的长为
(2)①设正方形ABCD的边长为a,正方形BEFG的边长为b,求图中阴影部分的面积(用含a和b的代数式表示)
②在①的条件下,如果a+b=20,ab=96,求阴影部分的面积.
考点:整式的混合运算,列代数式,代数式求值
专题:
分析:(1)利用两个正方形的面积,可求出AB与BE的长,即可得到AE的长.
(2)连接AG,利用阴影部分的面积=S△AGF+S△AGC求解即可,
(3)把面积
a2+
b2-
ab转化为
[(a+b)2-3ab],代入求解即可.
(2)连接AG,利用阴影部分的面积=S△AGF+S△AGC求解即可,
(3)把面积
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵两正方形的面积分别是9和4,
∴AB=3,BE=2,
∴AE=AB+BE=3+2=5,
故答案为:5.
(2)如图,连接AG,

阴影部分的面积=S△AGF+S△AGC
=
GF•BG+
CG•AB
=
b2+
(a-b)a.
=
a2+
b2-
ab.
(3)∵a+b=20,ab=96,
∴面积=
a2+
b2-
ab.
=
(a2+b2-ab),
=
[(a+b)2-3ab],
=
[202-3×96],
=
[400-288],
=
×112,
=56.
∴AB=3,BE=2,
∴AE=AB+BE=3+2=5,
故答案为:5.
(2)如图,连接AG,

阴影部分的面积=S△AGF+S△AGC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵a+b=20,ab=96,
∴面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=56.
点评:本题主要考查了整式的混合运算,列代数式及求值,解题的关键是能把不规则图形转化为规则图形求面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
a表示有理数,则-a一定是( )
| A、负数 | B、正数 |
| C、正数或负数 | D、以上都不对 |
 已知,如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,CD的垂直平分线分别交AC,CD,BC于点E,O,F.求证:四边形CEDF是正方形.
已知,如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,CD的垂直平分线分别交AC,CD,BC于点E,O,F.求证:四边形CEDF是正方形. 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点O,试说明:
如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点O,试说明: 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB=
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB=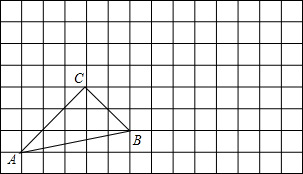 如图,在一个边长为1的正方形网格上,把△ABC向右平移4个方格,再向上平移2个方格,得到△A′B′C′(A′、B′、C′分别对应A、B、C).
如图,在一个边长为1的正方形网格上,把△ABC向右平移4个方格,再向上平移2个方格,得到△A′B′C′(A′、B′、C′分别对应A、B、C). 如图,在△ABC中,AB=15,BC=14,AC=13.求这个三角形的面积.
如图,在△ABC中,AB=15,BC=14,AC=13.求这个三角形的面积.