题目内容
 已知,如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,CD的垂直平分线分别交AC,CD,BC于点E,O,F.求证:四边形CEDF是正方形.
已知,如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,CD的垂直平分线分别交AC,CD,BC于点E,O,F.求证:四边形CEDF是正方形.考点:正方形的判定
专题:证明题
分析:首先根据垂直平分线的性质得到EC=ED,FC=FD,然后根据∠ACB=90°,CD平分∠ACB,得到∠ACD=∠BCD=45°,从而得到ED=EC=CF=FD,进而判定四边形CEDF为菱形,利用有一个角是直角的菱形是平行四边形判定正方形即可.
解答:证明:∵CD的垂直平分线分别交AC,CD,BC于点E,O,F,
∴EC=ED,FC=FD,
∵∠ACB=90°,CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴ED=EC=CF=FD,
∴四边形CEDF为菱形,
∵∠ACB=90°,
∴四边形CEDF为正方形.
∴EC=ED,FC=FD,
∵∠ACB=90°,CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴ED=EC=CF=FD,
∴四边形CEDF为菱形,
∵∠ACB=90°,
∴四边形CEDF为正方形.
点评:本题考查了正方形的判定,解题的关键是了解判定正方形时要判定该四边形既是菱形又是正方形,难度不大.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
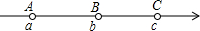 如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )| A、点A的左边 |
| B、点A与点B之间 |
| C、点B与点C之间 |
| D、点B与点C之间(靠近点C)或点C的右边 |
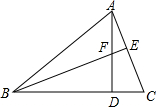 △ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )
△ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )| A、2 | B、3 | C、4 | D、5 |
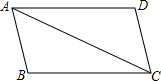 如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )
如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )| A、SAS | B、ASA |
| C、AAS | D、以上都不对 |
 如图,有一块三角形土地,AC=6m,BC=4m,∠B=60°,则这块土地的面积为
如图,有一块三角形土地,AC=6m,BC=4m,∠B=60°,则这块土地的面积为 如图,已知实数a、b在数轴上的对应点的位置如图所示,化简:|b|-
如图,已知实数a、b在数轴上的对应点的位置如图所示,化简:|b|-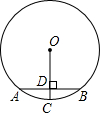 如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦12.如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是
如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦12.如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是 小明写作业时,不慎将墨水滴在数轴上,根据图中数值,请你确定墨迹盖住部分的整数共有
小明写作业时,不慎将墨水滴在数轴上,根据图中数值,请你确定墨迹盖住部分的整数共有 如图,正方形ABCD和正方形BEFG平放在一起.
如图,正方形ABCD和正方形BEFG平放在一起.