题目内容
如图，△ABC≌△BAD，点A和点B，点C和点D是对应点．如果∠D=70°，∠CAB=50°，那么∠DAB=考点：全等三角形的性质
专题：
分析：根据全等三角形的对应角相等，即可求得∠DBA的度数，然后根据三角形的内角和定理即可求出∠DAB的度数．
解答：解：∵△ABC≌△BAD，点A和点B、点C和点D是对应点，
∴∠CAB的对应角是∠DBA，
∴∠CAB=∠DBA=50°．
∵∠D+∠DBA+∠DAB=180°，∠D=70°，
∴∠DAB=180°-70°-50°=60°．
故答案为：60°．
∴∠CAB的对应角是∠DBA，
∴∠CAB=∠DBA=50°．
∵∠D+∠DBA+∠DAB=180°，∠D=70°，
∴∠DAB=180°-70°-50°=60°．
故答案为：60°．
点评：此题主要考查的是全等三角形的性质，找准对应角是解答此题的关键．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
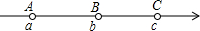如图，数轴上的A，B，C三点所表示的数是分别是a、b、c，其中AB=BC，如果|a|＞|b|＞|c|，那么该数轴的原点O的位置应该在（ ）| A、点A的左边 |
| B、点A与点B之间 |
| C、点B与点C之间 |
| D、点B与点C之间（靠近点C）或点C的右边 |
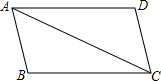如图，已知AB∥DC，AD∥BC，则△ABC≌△CDA的依据是（ ）| A、SAS | B、ASA |
| C、AAS | D、以上都不对 |
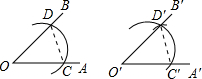如图，用尺规作图作“一个角等于已知角”的原理是：因为△D′O′C′≌△DOC，所以∠D′O′C′=∠DOC．由这种作图方法得到的△D′O′C′和△DOC全等的依据是
如图，若sinα=
如图，正方形ABCD和正方形BEFG平放在一起．下列说法中，正确的是（ ）
| A、一个数的立方根有两个，它们互为相反数 |
| B、负数没有立方根 |
| C、一个数的立方根比平方根小 |
| D、0的立方根仍为0 |