题目内容
 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点O,试说明:
如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点O,试说明:(1)∠BOC=180°-
| 1 |
| 2 |
(2)∠BOC=90°+
| 1 |
| 2 |
考点:三角形内角和定理,三角形的外角性质
专题:证明题
分析:(1)根据角平分线定义得到∠1=
∠ABC,∠2=
∠ACB,再根据三角形内角和定理得∠BOC=180°-∠1-∠2,所以∠APB=180°-
(∠ABC+∠ACB);
(2)根据三角形内角和定理得∠ABC+∠ACB=180°-∠A,所以∠BOC=180°-
(180°-∠A),然后整理即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形内角和定理得∠ABC+∠ACB=180°-∠A,所以∠BOC=180°-
| 1 |
| 2 |
解答:证明:(1)∠ABC与∠ACB的平分线交于点O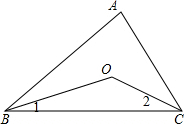 ,
,
∴∠1=
∠ABC,∠2=
∠ACB,
∵∠BOC=180°-∠1-∠2,
∴∠APB=180°-
(∠ABC+∠ACB);
(2)∵∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-
(180°-∠A)
=90°+
∠A.
 ,
,∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BOC=180°-∠1-∠2,
∴∠APB=180°-
| 1 |
| 2 |
(2)∵∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线定义和角的计算.此题揭示了∠BOC与∠A的数量关系.

练习册系列答案
相关题目
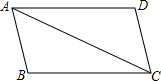 如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )
如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )| A、SAS | B、ASA |
| C、AAS | D、以上都不对 |
 如图,已知实数a、b在数轴上的对应点的位置如图所示,化简:|b|-
如图,已知实数a、b在数轴上的对应点的位置如图所示,化简:|b|- 小明写作业时,不慎将墨水滴在数轴上,根据图中数值,请你确定墨迹盖住部分的整数共有
小明写作业时,不慎将墨水滴在数轴上,根据图中数值,请你确定墨迹盖住部分的整数共有 如图在正方体的展开图上编号,请写出相对面(相对面没有公共棱)的号码:1对应
如图在正方体的展开图上编号,请写出相对面(相对面没有公共棱)的号码:1对应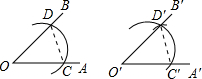 如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC.由这种作图方法得到的△D′O′C′和△DOC全等的依据是
如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC.由这种作图方法得到的△D′O′C′和△DOC全等的依据是 如图,正方形ABCD和正方形BEFG平放在一起.
如图,正方形ABCD和正方形BEFG平放在一起.