题目内容
 如图,在△ABC中,AB=15,BC=14,AC=13.求这个三角形的面积.
如图,在△ABC中,AB=15,BC=14,AC=13.求这个三角形的面积.考点:勾股定理
专题:
分析:过点A作AD⊥BC于点D,设BD=x,则CD=14-x,再根据勾股定理求出x的值,进而可得出AD的长,由三角形的面积公式即可得出结论.
解答: 解:过点A作AD⊥BC于点D,设BD=x,则CD=14-x,
解:过点A作AD⊥BC于点D,设BD=x,则CD=14-x,
∵△ADB与△ACD均为直角三角形,
∴AB2-BD2=AC2-CD2,即152-x2=132-(14-x)2,解得x=9,
∴AD=
=
=12,
∴S△ABC=
BC•AD=
×14×12=84.
 解:过点A作AD⊥BC于点D,设BD=x,则CD=14-x,
解:过点A作AD⊥BC于点D,设BD=x,则CD=14-x,∵△ADB与△ACD均为直角三角形,
∴AB2-BD2=AC2-CD2,即152-x2=132-(14-x)2,解得x=9,
∴AD=
| AB2-BD2 |
| 152-92 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
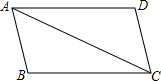 如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )
如图,已知AB∥DC,AD∥BC,则△ABC≌△CDA的依据是( )| A、SAS | B、ASA |
| C、AAS | D、以上都不对 |
下列说法中,正确的是( )
| A、一个数的立方根有两个,它们互为相反数 |
| B、负数没有立方根 |
| C、一个数的立方根比平方根小 |
| D、0的立方根仍为0 |
 如图,正方形ABCD和正方形BEFG平放在一起.
如图,正方形ABCD和正方形BEFG平放在一起. 如图,一个多面体的展开图中,每个面内的大写字母表示该面,被剪开的棱边所注的小写字母可表示该棱.
如图,一个多面体的展开图中,每个面内的大写字母表示该面,被剪开的棱边所注的小写字母可表示该棱.