题目内容
2.已知关于x的方程x2+(2k+1)x+k2=0的两个实数根的平方和是7,则k=-3或1.分析 由方程x2+(2k+1)x+k2=0的两个实数根的平方和为7,利用根与系数的关系列出方程,求出方程的即即可得到k的值.
解答 解:∵方程x2+(2k+1)x+k2=0的两个实数根的平方和是7,
∴x1+x2=-2k-1,x1x2=k2,
∵x12+x22=7,
∴(x1+x2)2-2x1x2=(2k+1)2-2k2=7,
整理得:2k2+4k-6=0,
分解因式得:(2k+6)(k-1)=0,
解得:k=-3或k=1,
故答案为:-3或1
点评 此题考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
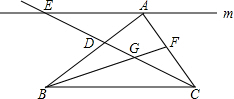 如图,点G是△ABC的重心,直线m过点A且与BC平行,若射线CG分别交直线m及线段AB于E、D两点,则S△AED:S四边形ADGF=3:2.
如图,点G是△ABC的重心,直线m过点A且与BC平行,若射线CG分别交直线m及线段AB于E、D两点,则S△AED:S四边形ADGF=3:2.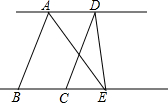 如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为20.
如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为20.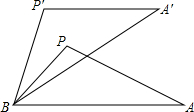 如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$)
如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$)