题目内容
11. 如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$)
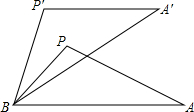
如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$)
分析 连接AA′,过B作BC⊥AA′于点C,由题意知BA=BA′,再根据等腰三角形底边上高也是底边上的中线和顶角的平分线得到∠ABC=15°,最后利用AC=ABsin15°和已知条件即可求出AA′.
解答  解:如图,连接AA′,过B作BC⊥AA′于点C.
解:如图,连接AA′,过B作BC⊥AA′于点C.
∵△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,
∴BA=BA′,∠ABA′=30°,
∵BC⊥AA′于点C,
∴∠ABC=15°,AA′=2AC.
∵在Rt△ABC中,∠ACB=90°,
∴AC=ABsin15°=4×$\frac{\sqrt{6}-\sqrt{2}}{4}$=$\sqrt{6}$-$\sqrt{2}$,
∴AA′=2AC=2$\sqrt{6}$-2$\sqrt{2}$.
故答案为2$\sqrt{6}$-2$\sqrt{2}$.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等腰三角形的性质以及锐角三角函数的定义.

练习册系列答案
相关题目
19. 如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
 如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
3.某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了三项测试,两人的三项测试成绩如表所示.根据实际需要,广播电视局将面试、笔试和上镜效果测试的得分按3:3:4的比例计算两人的总成绩,那么A(填A或B)将被录用.
| 测试项目测试成绩 | A | B |
| 面试 | 90 | 95 |
| 笔试 | 80 | 85 |
| 上镜效果 | 80 | 70 |
1.若一元二次方程x2-ax+3=0有两个实数根,则a的值可以是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

 如图,已知AB∥DE,点C是BE上的一点,∠A=∠BCA,∠D=∠DCE.求证:AC⊥CD.
如图,已知AB∥DE,点C是BE上的一点,∠A=∠BCA,∠D=∠DCE.求证:AC⊥CD.