题目内容
14.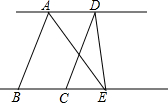 如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为20.
如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为20.
分析 作DG⊥BC,AH⊥BC,根据△DCE的面积为6,求出DG,根据两平行线间的距离相等得到AH的长,根据平行四边形的面积公式得到答案.
解答  解:作DG⊥BC于G,AH⊥BC于H,
解:作DG⊥BC于G,AH⊥BC于H,
∵AD∥BC,∴AH=DG,
又AB∥CD,
∴四边形ABCD是平行四边形,
∴BC=AD=5,又BE=8,
∴CE=3,又△DCE的面积为6,
∴DG=4,
∴四边形ABCD的面积=BC×AH=20,
故答案为:20.
点评 本题考查的是平行线间的距离,掌握两平行线间的距离相等和平行四边形的性质以及面积公式是解题的关键.

练习册系列答案
相关题目
19. 如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
 如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
3.某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了三项测试,两人的三项测试成绩如表所示.根据实际需要,广播电视局将面试、笔试和上镜效果测试的得分按3:3:4的比例计算两人的总成绩,那么A(填A或B)将被录用.
| 测试项目测试成绩 | A | B |
| 面试 | 90 | 95 |
| 笔试 | 80 | 85 |
| 上镜效果 | 80 | 70 |
4.在△ABC中,D,E分别是AB,AC上的点,且DE∥BC,则下列结论不正确的是( )
| A. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | B. | $\frac{AB}{DB}$=$\frac{AC}{EC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{DB}$=$\frac{AC}{BC}$ |
 陈老师的汽车牌号在水中的倒影如左图,则陈老师的汽车牌号实际是J2126A.
陈老师的汽车牌号在水中的倒影如左图,则陈老师的汽车牌号实际是J2126A.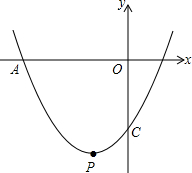 已知平面直角坐标系xOy,抛物线y=$\frac{1}{2}$x2+bx+c经过点A(-3,0)、C(0,-$\frac{3}{2}$).
已知平面直角坐标系xOy,抛物线y=$\frac{1}{2}$x2+bx+c经过点A(-3,0)、C(0,-$\frac{3}{2}$).