题目内容
10.梯形的底为a,b,且a>b,对角线长为c,d,且c>d,求面积.分析 过D点作AC的平行线交BC的延长线于E点,将梯形的上、下底的和,两条对角线平移到同一三角形中,用勾股定理的逆定理证明直角三角形,再将梯形面积转化为求△BDE的面积.
解答 解:如图,过D点作AC的平行线交BC的延长线于E点,过D作DM⊥BC于M,
∵AD∥BC,
∴四边形ACED为平行四边形,
∴AD=CE=b,AC=DE=c,
∴求梯形面积可转化为求△BDE的面积,
设BM=x,则EM=a+b-x,
由勾股定理得:c2-(a+b-x)2=d2-x2,
解得:x=$\frac{{d}^{2}-{c}^{2}+(a+b)^{2}}{2(a+b)}$,
∴DM=$\sqrt{{d}^{2}-(\frac{{d}^{2}-{c}^{2}+(a+b)^{2}}{2(a+b)})^{2}}$
∴梯形面积=三角形BDE的面积=$\frac{1}{2}$(a+b)$\sqrt{{d}^{2}-(\frac{{d}^{2}-{c}^{2}+(a+b)^{2}}{2(a+b)})^{2}}$.
点评 此题考查梯形,勾股定理,掌握梯形的性质与解决梯形问题常用作辅助线的方法是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.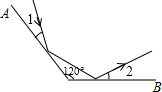 如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )
如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )
 如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )
如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
19. 如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
 如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )
如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C,若AC⊥A′B′,则∠A等于( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |

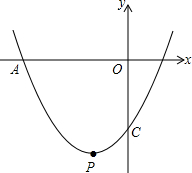 已知平面直角坐标系xOy,抛物线y=$\frac{1}{2}$x2+bx+c经过点A(-3,0)、C(0,-$\frac{3}{2}$).
已知平面直角坐标系xOy,抛物线y=$\frac{1}{2}$x2+bx+c经过点A(-3,0)、C(0,-$\frac{3}{2}$).