题目内容
14.先化简,再求值:$\frac{2y}{{x}^{2}-{y}^{2}}$-$\frac{1}{x-y}$,其中x=3$\sqrt{2}$-2,y=-2$\sqrt{2}$+1.分析 原式通分并利用同分母分式的减法法则计算,约分得到最简结果,把x与y的值代入计算即可求出值.
解答 解:原式=$\frac{2y-(x+y)}{(x+y)(x-y)}$=$\frac{-(x-y)}{(x+y)(x-y)}$=-$\frac{1}{x+y}$,
当x=3$\sqrt{2}$-2,y=-2$\sqrt{2}$+1时,原式=-$\frac{1}{\sqrt{2}-1}$=-$\sqrt{2}$-1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.若(x-3)2=x2-mx+9,则m的值是( )
| A. | 3 | B. | 6 | C. | 9 | D. | -6 |
19.已知某一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数为( )
| A. | y=-x-2 | B. | y=-x+10 | C. | y=-x-6 | D. | y=-x-10 |
20.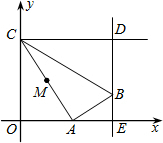 如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
 如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )
如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=$\frac{25}{4}$时,t的值为( )| A. | 2或2+3$\sqrt{2}$ | B. | 2或2+3$\sqrt{3}$ | C. | 3或3+5$\sqrt{3}$ | D. | 3或3+5$\sqrt{2}$ |
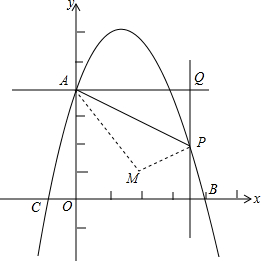 已知抛物线y=-x2+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l.在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
已知抛物线y=-x2+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l.在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.