题目内容
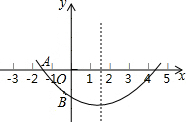 关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )
关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )| A、①② | B、①③ | C、③ | D、①②③ |
考点:二次函数图象与系数的关系
专题:数形结合
分析:观察图象得x=
时,y<0,即
a-
b+c<0,则可对①进行判断;
先得到A(c,0),再根据二次函数图象上点的坐标特征得到ac2+bc+c=0,且-2<c<-1,变形得到a=-
,再由对称轴的位置得到2a+b<0,消去a得-
+b<0,可解得b>
,所以-
<b<-
,于是可对②进行判断;
由于c=-
,-2<c<-1,则-2<-
<-1,变形后有b>a-1,加上b<0,所以a-1<0,则可对③进行判断.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
先得到A(c,0),再根据二次函数图象上点的坐标特征得到ac2+bc+c=0,且-2<c<-1,变形得到a=-
| b+1 |
| c |
| 2b+2 |
| c |
| 2 |
| c-2 |
| 4 |
| 3 |
| 1 |
| 2 |
由于c=-
| b+1 |
| a |
| b+1 |
| a |
解答:解:∵x=
时,y<0,
∴
a-
b+c<0,即a-2b+4c<0,所以①正确;
∵B(0,c),OA=OB,
∴A(c,0),
∴ac2+bc+c=0,-2<c<-1,
∴ac+b+1=0,
∴a=-
∵1<-
<2,
∴2a+b<0,
∴-
+b<0,
∴b>
,
而-2<c<-1,
∴-
<b<-
,
∴c-4b>0,所以②错误;
∵c=-
,
∴-2<-
<-1,
∴-2a<-b-1<-a,
∴b>a-1,
而b<0,
∴a-1<0,
∴0<a<1,所以③正确.
故选B.
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
∵B(0,c),OA=OB,
∴A(c,0),
∴ac2+bc+c=0,-2<c<-1,
∴ac+b+1=0,
∴a=-
| b+1 |
| c |
∵1<-
| b |
| 2a |
∴2a+b<0,
∴-
| 2b+2 |
| c |
∴b>
| 2 |
| c-2 |
而-2<c<-1,
∴-
| 4 |
| 3 |
| 1 |
| 2 |
∴c-4b>0,所以②错误;
∵c=-
| b+1 |
| a |
∴-2<-
| b+1 |
| a |
∴-2a<-b-1<-a,
∴b>a-1,
而b<0,
∴a-1<0,
∴0<a<1,所以③正确.
故选B.
点评:本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
计算:
-
=( )
4+
|
4-
|
A、
| ||
B、
| ||
| C、2 |
分式
与
的最简公分母为( )
| 1 |
| x2-y2 |
| 1 |
| y-x |
| A、x-y |
| B、x+y |
| C、x2-y2 |
| D、(x2-y2)(y-x) |
小明使用电脑编了如下一个程序:
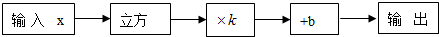
已知当输入x的值是2时,输出的值为-14,当输入x的值是-2时,输出的值为18,则当输入x的值为
时,输出的值为( )
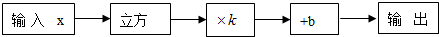
已知当输入x的值是2时,输出的值为-14,当输入x的值是-2时,输出的值为18,则当输入x的值为
| 1 |
| 2 |
A、1
| ||
B、-1
| ||
C、1
| ||
D、1
|
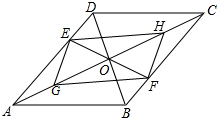 如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.
如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形. 如图,为测量某广告牌面积,小明同学在广告牌正下方的观测点P的B,C,D的仰角分别为30°,45°,65°,若观测点P与广告牌右下角C的水平距离为6cm,你能根据以上数据求出广告牌的面积吗(结果取整数)?
如图,为测量某广告牌面积,小明同学在广告牌正下方的观测点P的B,C,D的仰角分别为30°,45°,65°,若观测点P与广告牌右下角C的水平距离为6cm,你能根据以上数据求出广告牌的面积吗(结果取整数)? 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G,写出图中两对相似三角形,并证明其中的一对.
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G,写出图中两对相似三角形,并证明其中的一对.