题目内容
5．两个边长分别为1，2，$\sqrt{5}$的三角形，拼成一个四边形，则能拼成几种不同的四边形．（ ）| A． | 2种 | B． | 3种 | C． | 4种 | D． | 5种 |
分析 首先利用勾股定理的逆定理得到两个三角形是直角三角形，然后拿两个“90°、60°、30°”的三角板试一试即可得．
解答 解：∵两个边长分别为1，2，$\sqrt{5}$的三角形，
∴12+22=（$\sqrt{5}$）2，
∴两三角形均为直角三角形，
有以下拼法：
共4种，
故选C．
点评 考查了图形的拼剪，要注意不同边的组合方式，不要遗漏任何一种可能性．本题是一个操作题，动手做一做即可．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
1．下列式子运算正确的是（ ）
| A． | a6÷a2=a4 | B． | a2+a3=a5 | C． | （a+1）2=a2+1 | D． | 3a-2a=1 |
5．在下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
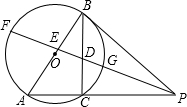已知：如图AB是⊙O的直径，PB切⊙O于点B，PA交⊙O于点C，PF分别交AB、BC于E、D，交⊙O于F、G，且BE、BD恰好是关于x的方程x2-6x+（m2+4m+13）=0（其中m为实数）的两根．
17．关于x的二次函数y=-（x-1）2+2，下列说法正确的是（ ）
| A． | 当x＞1时，y随x的增大而减小 | B． | 图象与y轴的交点坐标为（0，2） | ||
| C． | 图象的开口向上 | D． | 图象的顶点坐标是（-1，2） |