题目内容
 如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=
如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=| 1 |
| 4 |
| 1 |
| 9 |
| AB |
| CD |
考点:二次函数图象上点的坐标特征
专题:
分析:把P点的纵坐标分别代入C1、C2的解析式就可以AB、CD的值,就可以求出结论;
解答:解:将点P的纵坐标y=m2(m>0)代入y=
x2得x=±2m,
∴A(-2m,m2),B(2m,m2),
∴AB=4m.
将y=m2(m>0)代入:y=
x2得x=±3m,
∴C(-3m,m2),D(3m,m2),
∴CD=6m.
∴
=
=
;
| 1 |
| 4 |
∴A(-2m,m2),B(2m,m2),
∴AB=4m.
将y=m2(m>0)代入:y=
| 1 |
| 9 |
∴C(-3m,m2),D(3m,m2),
∴CD=6m.
∴
| AB |
| CD |
| 4 |
| 6 |
| 2 |
| 3 |
点评:本题考查了二次函数图象上点的坐标特征,对称轴为y轴的抛物线的性质的运用,根据P的坐标求得AB、CD的长是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
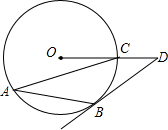 如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )
如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )| A、54° | B、44° |
| C、27° | D、22° |
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;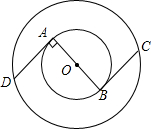 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=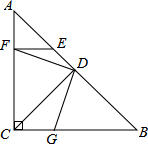 已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.
已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.