题目内容
4. 如图,?ABCD中,E是AB的中点,AB=10,AC=9,DE=12,则△CDE的面积S=36.
如图,?ABCD中,E是AB的中点,AB=10,AC=9,DE=12,则△CDE的面积S=36.
分析 作AF∥DE交CD延长线于F,得出四边形AFDE是平行四边形,求得CF2=AF2+AC2,即△ACF是直角三角形,根据直角三角形的面积求得?ABCD的CD边上的高,即可得出结果
解答 解:作AF∥DE交CD延长线于F,如图所示: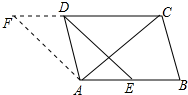
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴AE∥DF,
∴四边形AFDE是平行四边形,
∴AF=DE=12,DF=AE=$\frac{1}{2}$AB=5,CF=CD+DF=10+5=15,
∵152=122+92,
即:CF2=AF2+AC2,
∴△ACF是直角三角形,
∴?ABCD的CD边上的高=$\frac{12×9}{15}$=$\frac{36}{5}$,
∴?ABCD的面积=AB×高=10×$\frac{36}{5}$=72.
∴△CDE的面积=$\frac{1}{2}$×72=36;
故答案为36.
点评 本题考查了平行四边形的性质与判定、勾股定理的逆定理、平行四边形面积的计算;熟练掌握平行四边形的判定与性质,由勾股定理的逆定理证明△ACF是直角三角形是解决问题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13. 如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )
如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )
 如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )
如图,A、B、C三点在⊙O上,若∠B=53°,∠A=21°,则∠AOB等于( )| A. | 32° | B. | 53° | C. | 64° | D. | 74° |
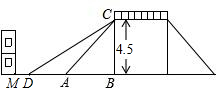 如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)
如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)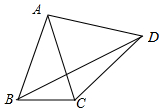 如图,△ABC中,AB=AC=5,BC=2,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD=$\sqrt{3}$+2$\sqrt{6}$.
如图,△ABC中,AB=AC=5,BC=2,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD=$\sqrt{3}$+2$\sqrt{6}$. 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD若∠A=28°,则∠C=34度.
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD若∠A=28°,则∠C=34度.