Question

14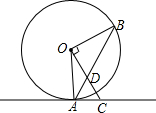．如图，点A，B在⊙O上，直线AC是⊙O的切线，OC⊥OB，连接AB交OC于点D．求证：AC=CD．

Answer 1

分析 AC为圆的切线，利用切线的性质得到∠OAC为直角，再由OC与OB垂直，得到∠BOC为直角，由OA=OB，利用等边对等角得到一对角相等，再利用对顶角相等及等角的余角相等得到一对角相等，利用等角对等边即可得证．

解答 ∵直线AC与⊙O相切，
∴OA⊥AC，
∴∠OAC=90°，即∠OAB+∠CAB=90°，
∵OC⊥OB，
∴∠BOC=90°，
∴∠B+∠ODB=90°，
而∠ODB=∠ADC，
∴∠ADC+∠B=90°，
∴OA=OB，
∴∠OAB=∠B，
∴∠ADC=∠CAB，
∴AC=CD．

点评 此题考查了切线的性质，勾股定理，等腰三角形的性质，熟练掌握切线的性质是解本题的关键．