题目内容
16.解下列方程(1)x-4=2-5x
(2)1-$\frac{2x-5}{6}$=$\frac{3-x}{4}$
(3)y-$\frac{y+1}{2}$=2-$\frac{y+2}{5}$.
(4)$\frac{2}{3}$(2t-6)-$\frac{1}{2}$(2t-4)=4.
(5)$\frac{0.4x+0.9}{0.5}$-$\frac{0.03+0.02x}{0.03}$=$\frac{x-5}{2}$.
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把y系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把t系数化为1,即可求出解;
(5)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)移项合并得:6x=6,
解得:x=1;
(2)去分母得:12-2(2x-5)=3(3-x),
去括号得:12-4x+10=9-3x,
移项合并得:-x=-13,
解得:x=13;
(3)去分母得:10y-5(y+1)=20-2(y+2),
去括号得:10y-5y-5=20-2y-4,
移项得:10y-5y+2y=20-4+5,
合并同类项得:7y=21,
解得:y=3;
(4)去分母得,4(2t-6)-3(2t-4)=24,
去括号得,8t-24-6t+12=24,
移项得,8t-6t=24+24-12,
合并同类项得,2t=36,
系数化为1得,t=18
(5)整理,得$\frac{4x+9}{5}$-$\frac{3+2x}{3}$=$\frac{x-5}{2}$,
去分母,得6(4x+9)-10(3+2x)=15(x-5),
去括号,得24x+54-30-20x=15x-75,
移项,得24x-20x-15x=-75-54+30,
合并,得-11x=-99,
系数化为1,得x=9.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.关于x的一元二次方程(m-1)x2+2mx+m=0有实数根,则m的取值范围是( )
| A. | x≥0 | B. | x≥0且≠1 | C. | m≠1 | D. | m>1 |
6.一元二次方程x2-81=0的解是( )
| A. | x1=x2=9 | B. | x1=x2=-9 | C. | x1=-9,x2=9 | D. | x1=-1,x2=2 |
 根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为1.
根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为1.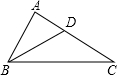 如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$.
如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$.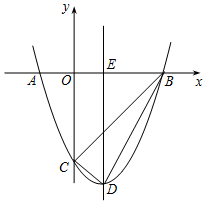 如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.