题目内容
13.设△ABC的外接圆O上的劣弧$\widehat{BC}$的中点为K,优弧$\widehat{BC}$的中点为S,线段AK与边BC交于点D,点E,F分别为△ACD,△ABD的外心.试证:A,E,O,F,S五点共圆.分析 如图,连接SB、SC、SK、AS、OA,作AB的垂直平分线交SB于F′,连接AF′,DF′,作AC的垂直平分线交SC于E′,连接AE′,设AB交SK于G.首先证明A,E′,O,F′,S五点共圆,再利用重合法证明点F′是△ABD的外心,点E′是△ADC的外心,推出F与F′重合,E与E′重合,即可解决问题.
解答 证明:如图,连接SB、SC、SK、AS、OA,作AB的垂直平分线交SB于F′,连接AF′,DF′,作AC的垂直平分线交SC于E′,连接AE′,设AB交SK于G.
∵劣弧$\widehat{BC}$的中点为K,优弧$\widehat{BC}$的中点为S,
∴SK经过圆心O,
∵F′B=F′A,OK=OA,
∴∠F′BA=∠F′AB,∠K=∠OAK,
∵∠SF′A=2∠F′BA,∠SOA=2∠K,
∴∠SF′A=∠SOA,
∴S、F′、O、A四点共圆,同理可证S、O、E′、A四点共圆,
∴A,E′,O,F′,S五点共圆,
∴∠SAF′=∠SOF′,
∵∠SOF′+∠BGO=90°,∠BGO+∠ABC=90°,
∴∠SOF′=∠ABC=∠ASC=∠SAF′,
∵∠AF′S=∠SE′A,AS=SA,
∴△SAF′≌△SAE′,
∴AF′=AE′,
∵∠F′BA=∠F′AB=∠ACE′=∠CAE′,
∴△AF′B∽△AE′C,
∴$\frac{AB}{AC}$=$\frac{BF′}{AE′}$=$\frac{BF′}{SF′}$,
∵$\widehat{BK}$=$\widehat{CK}$,
∴∠BAD=∠DAC,
∴$\frac{AB}{AC}$=$\frac{BD}{DC}$,
∴$\frac{BD}{DC}$=$\frac{BF′}{SF′}$,
∴DF′∥SC,
∴∠F′DB=∠SCB,
∵SB=SC,
∴∠F′BD=∠SCB=∠F′DB,
∴F′B=F′D=F′A,
∴点F′是△ABD的外心,同理可证E′是△ADC的外心,
∴F与F′重合,E与E′重合,
∴A,E,O,F,S五点共圆.
点评 本题考查相似三角形的判定和性质、四点共圆、全等三角形的判定和性质、三角形的外心与外接圆、平行线的判定等知识,解题的关键是学会利用重合法解决问题,学会添加常用辅助线,构造全等三角形解决问题,题目比较难,属于竞赛题.

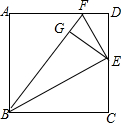 如图,正方形ABCD中,点E是CD的中点,DF=$\frac{1}{4}$AD,EG⊥BF于G,求证:BE2=BG•BF.
如图,正方形ABCD中,点E是CD的中点,DF=$\frac{1}{4}$AD,EG⊥BF于G,求证:BE2=BG•BF. 如图,已知函数y=2x和y=ax-3的图象交于点P(-1,-2),则根据图象可得不等式2x-ax+3>0的解集是-1.
如图,已知函数y=2x和y=ax-3的图象交于点P(-1,-2),则根据图象可得不等式2x-ax+3>0的解集是-1.