题目内容
9.若方程ax2-bx+8=x是关于x的一元一次方程,则a,b的值必须满足( )| A. | a=0,b≠-1 | B. | a=0,b≠0 | C. | a≠0,b=-1 | D. | a≠0,b≠0 |
分析 根据一元一次方程的定义,可得答案.
解答 解:由ax2-bx+8=x是关于x的一元一次方程,得
a=0且b+1≠0,
解得a=0且b≠-1,
故选:A.
点评 本题考查了一元一次方程的概念和解法.一元一次方程的未知数的指数为1.

练习册系列答案
相关题目
19.计算:
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
20. 如图,图中共有同旁内角( )
如图,图中共有同旁内角( )
 如图,图中共有同旁内角( )
如图,图中共有同旁内角( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
4.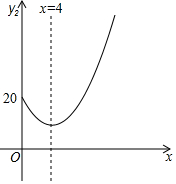 已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
7~10月份的销售单价y2(元/千克)与时间x(月)满足函数关系:y2=x2+bx+c,其图象如图.今年1~6月份的月销量z1(万千克)与时间x(月)满足关系式:z1=-x2+6x;而7~10月份的月销量一直稳定在8万千克.
(1)请观察题目中的表格及图象,直接写出y1(元/千克)与时间x(月)的函数关系式及y2(元/千克)与时间x(月)的函数关系式.
(2)求出该种水果今年1~10月哪个月的销售额最大?最大销售额为多少万元?
(3)进入11月后,商场决定将销售单价在取得最大月销售额时的单价的基础上提高2a%,预测月销售量将在取得最大月销售额时的销售量的基础上下降0.5a%,若要使该种水果11月份的销售额达到360万元,求出a的最小整数值(a<100)?(参考数据:$\sqrt{6}$≈2.45;$\sqrt{7}$≈2.65;$\sqrt{8}$≈2.83)
 已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y1 | 60 | 30 | 20 | 15 | 12 | 10 |
(1)请观察题目中的表格及图象,直接写出y1(元/千克)与时间x(月)的函数关系式及y2(元/千克)与时间x(月)的函数关系式.
(2)求出该种水果今年1~10月哪个月的销售额最大?最大销售额为多少万元?
(3)进入11月后,商场决定将销售单价在取得最大月销售额时的单价的基础上提高2a%,预测月销售量将在取得最大月销售额时的销售量的基础上下降0.5a%,若要使该种水果11月份的销售额达到360万元,求出a的最小整数值(a<100)?(参考数据:$\sqrt{6}$≈2.45;$\sqrt{7}$≈2.65;$\sqrt{8}$≈2.83)
1.下面关于五棱柱的说法错误的是( )
| A. | 有15条棱 | B. | 有10个顶点 | C. | 有15个顶点 | D. | 有7个面 |
18.下列各式由左边到右边的变形中,是分解因式的为( )
| A. | a (x+y)=a x+a y | B. | x2-4x+4=x(x-4)+4 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+3x=(x-4)(x+4)+3x |
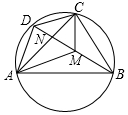 已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证:
已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证: 如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①a>0,b<0;②a-b<0;③a+b>0;④|a|-|b|>0,其中正确的有( )
如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①a>0,b<0;②a-b<0;③a+b>0;④|a|-|b|>0,其中正确的有( )