题目内容
7.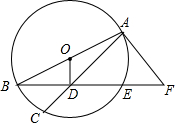 如图,AB是⊙O的直径,点E为弧AC的中点,AC、BE交于点D过A的切线交BE的延长线于F.
如图,AB是⊙O的直径,点E为弧AC的中点,AC、BE交于点D过A的切线交BE的延长线于F.(1)求证:AD=AF;
(2)若$\frac{AO}{AF}$=$\frac{2}{3}$,求tan∠ODA的值.
分析 (1)连接BC,由点E为弧AC的中点,得到∠ABE=∠CBE,由AF是⊙O的切线,得到∠BAF=90°,根据余角的性质得到∠BDC=∠F,等量代换得到∠ADE=∠F,于是得到结论;
(2)连接AE,由AB是⊙O的直径,得到AE⊥BF,根据等腰三角形的性质得到∠DAE=∠FAE,根据平行线的性质得到∠DAE=∠ADO,根据已知条件设AO=2x,AF=3x,勾股定理得到BF=5x,根据射影定理得到EF=$\frac{A{F}^{2}}{BF}$=$\frac{16}{5}$x,根据三角形的面积公式得到AE=$\frac{12}{5}$x,于是得到结论.
解答 解:(1)连接BC,
∵点E为弧AC的中点,
∴∠ABE=∠CBE,
∵AF是⊙O的切线,
∴∠BAF=90°,
∴∠ABF+∠F=90°,
∵AB是⊙O的直径,
∴∠C=90°,
∴∠CBD=∠BDC=90°,
∴∠BDC=∠F,
∵∠ADF=∠BDC,
∴∠ADE=∠F,
∴AD=AF;
(2)连接AE,
∵AB是⊙O的直径,
∴AE⊥BF,
∴∠DAE=∠FAE,
∵OD⊥BE,
∴OD∥AE,
∴∠DAE=∠ADO,
∴∠FAE=∠ODA,
∵$\frac{AO}{AF}$=$\frac{2}{3}$,
设AO=2x,AF=3x,
∴AB=4x,
∴BF=5x,
∵∠BAF=90°,AE⊥BF,
∴AF2=EF•BF,
∴EF=$\frac{A{F}^{2}}{BF}$=$\frac{16}{5}$x,
∵S△ABF=$\frac{1}{2}$AB•AF=$\frac{1}{2}$BF•AE,
∴AE=$\frac{12}{5}$x,
∴tan∠ODA=tan∠EAF=$\frac{EF}{AE}$=$\frac{4}{3}$.
点评 本题考查了圆周角定理,射影定理,三角形的面积公式,平行线的判定和性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案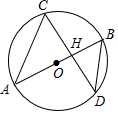 如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )
如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{7}{6}$ |
| A. | 1尾 | B. | 50尾 | C. | 500尾 | D. | 1 000尾 |
| 编号 | 教学方式 | 最喜欢的频数 | 频率 |
| 1 | 教师讲,学生听 | 20 | 0.10 |
| 2 | 教师提出问题,学生探索思考 | ||
| 3 | 学生自行阅读教材,独立思考 | 30 | |
| 4 | 分组讨论,解决问题 | 0.25 |

(1)收回的问卷份数为200,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.


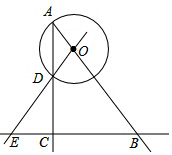 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E.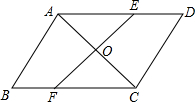 如图,四边形ABCD中,AD∥BC,∠B=∠D,点E、F分别在AD、BC上,EF与AC相交于点O.
如图,四边形ABCD中,AD∥BC,∠B=∠D,点E、F分别在AD、BC上,EF与AC相交于点O.