题目内容
15.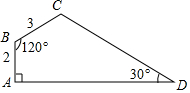 如图,四边形ABCD中,∠A=90°,∠B=120°,∠D=30°,AB=2,BC=3,则CD=7.
如图,四边形ABCD中,∠A=90°,∠B=120°,∠D=30°,AB=2,BC=3,则CD=7.
分析 先延长AB、DC交于E,根据已知证出△EBC是等边三角形,得出CE=BE=BC=3,求出AE=AB+BE=5,由直角三角形的性质得出DE=2AE=10,即可得出结果.
解答 解:延长AB、DC交于E,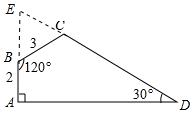
∵∠D=30°,∠A=90°,
∴∠E=60°,
∵∠ABC=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴CE=BE=BC=3,
∴AE=AB+BE=5,
∴DE=2AE=10,
∴CD=DE-CE=10-3=7;
故答案为:7.
点评 此题考查了含30度角的直角三角形的性质、等边三角形的判定与性质;熟练掌握含30°角的直角三角形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
4.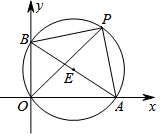 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )| A. | $\sqrt{6}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{6}+\sqrt{2}$ | D. | $1+\sqrt{3}$ |
5.有理数$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
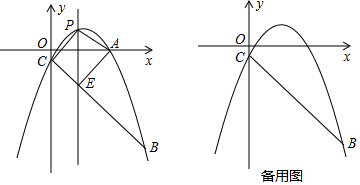
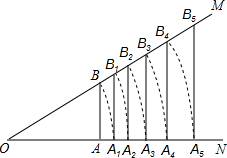 如图,已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1,过点A2作A2B2∥AB,A2B2交射线OM于点B2;…依次进行下去,则A1B1线段的长度为$\frac{2\sqrt{3}}{3}$,A6B6线段的长度为${2}^{6}(\frac{\sqrt{3}}{3})^{6}$.
如图,已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1,过点A2作A2B2∥AB,A2B2交射线OM于点B2;…依次进行下去,则A1B1线段的长度为$\frac{2\sqrt{3}}{3}$,A6B6线段的长度为${2}^{6}(\frac{\sqrt{3}}{3})^{6}$.