题目内容
14. 如图,已知点A是双曲线y=$\frac{{\sqrt{3}}}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是-3$\sqrt{3}$.
如图,已知点A是双曲线y=$\frac{{\sqrt{3}}}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是-3$\sqrt{3}$.
分析 设点A的坐标为(a,$\frac{\sqrt{3}}{a}$),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,进而得出结论.
解答 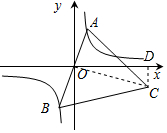 解:设A(a,$\frac{\sqrt{3}}{a}$),
解:设A(a,$\frac{\sqrt{3}}{a}$),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=$\sqrt{3}$AO,
∵AO=$\sqrt{{a}^{2}+\frac{3}{{a}^{2}}}$,
∴CO=$\sqrt{3{a}^{2}+\frac{9}{{a}^{2}}}$,
如图,过点C作CD⊥x轴于点D,则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,
即$\frac{\frac{\sqrt{3}}{a}}{a}$=$\frac{x}{-y}$,
解得y=-$\frac{\sqrt{3}}{3}$a2x.
在Rt△COD中,CD2+OD2=OC2,
即y2+x2=3a2+$\frac{9}{{a}^{2}}$,
将y=-$\frac{\sqrt{3}}{3}$a2x代入,可得:
x2=$\frac{9}{{a}^{2}}$,
故x=$\frac{3}{a}$,y=-$\sqrt{3}$a,
则xy=-3$\sqrt{3}$,即k=-3$\sqrt{3}$.
故答案为:-3$\sqrt{3}$.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
17.正方形的正投影不可能是( )
| A. | 线段 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
6.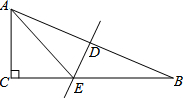 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )| A. | 15 | B. | 15$\sqrt{2}$ | C. | 30 | D. | 30$\sqrt{2}$ |
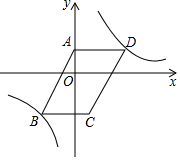 如图,在平面直角坐标系xOy中,双曲线y=$\frac{k}{x}$经过?ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,S?ABCD=5.
如图,在平面直角坐标系xOy中,双曲线y=$\frac{k}{x}$经过?ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,S?ABCD=5.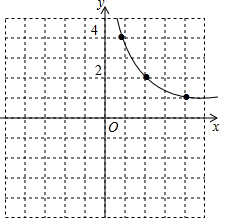 已知反比例函数y=$\frac{k}{x}$,图中已经画出了此函数图象的其中一支,请根据图中所给信息,把这个反比例函数图象的另一支补充完整.
已知反比例函数y=$\frac{k}{x}$,图中已经画出了此函数图象的其中一支,请根据图中所给信息,把这个反比例函数图象的另一支补充完整.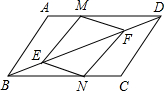 如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.
如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形. 如图所示,在△ABC中:
如图所示,在△ABC中: