题目内容
13. 已知AD为△ABC外角平分线,且点D在线段BC的垂直平分线上,DE⊥AB,tan∠BDC=$\frac{3}{4}$,BC=$\sqrt{10}$,AC=3,则AE=2.
已知AD为△ABC外角平分线,且点D在线段BC的垂直平分线上,DE⊥AB,tan∠BDC=$\frac{3}{4}$,BC=$\sqrt{10}$,AC=3,则AE=2.
分析 如图,作DH⊥CA于H,CM⊥AB于M,A交CD于O.由Rt△BDE≌Rt△CDH,推出AB=CH,∠DBO=∠ACO,由∠DOB=∠AOC,推出∠BDO=∠OAC,推出tan∠CAM=tan∠BDC=$\frac{3}{4}$=$\frac{CM}{AM}$,由AC=3,推出CM=$\frac{9}{5}$,AM=$\frac{12}{5}$,在Rt△BCM中,BM=$\sqrt{B{C}^{2}-C{M}^{2}}$=$\sqrt{10-\frac{81}{25}}$=$\frac{13}{5}$,推出CH=AB=5,由Rt△DAE≌Rt△DAH,可得AE=AH=CH-AC=5-3=2.
解答 解:如图,作DH⊥CA于H,CM⊥AB于M,A交CD于O.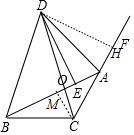
∵DE⊥ABAH⊥CA,
∴∠DEB=∠DHC=90°,
∵AD平分∠BAF,
∴DE=DH,
∵点D在线段BC的垂直平分线上
∴DB=DC,
∴Rt△BDE≌Rt△CDH,
∴AB=CH,∠DBO=∠ACO,∵∠DOB=∠AOC,
∴∠BDO=∠OAC,
∴tan∠CAM=tan∠BDC=$\frac{3}{4}$=$\frac{CM}{AM}$,∵AC=3,
∴CM=$\frac{9}{5}$,AM=$\frac{12}{5}$,
在Rt△BCM中,BM=$\sqrt{B{C}^{2}-C{M}^{2}}$=$\sqrt{10-\frac{81}{25}}$=$\frac{13}{5}$,
∴CH=AB=5,
∵AD=AD,DE=DH,
∴Rt△DAE≌Rt△DAH,
∴AE=AH=CH-AC=5-3=2.
故答案为2.
点评 本题考查角平分线的性质定理、线段的垂直平分线的性质、解直角三角形.全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造去对角线解决问题,属于中考常考题型.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案| A. | -7x<-7y | B. | 7-x>7-y | C. | x-7>y-7 | D. | x+7>y+7 |
 如图,Rt△ABE中,∠ABE=90°,BE=15,AE=17,以AB为边作正方形ABCD,则正方形ABCD的面积等于64.
如图,Rt△ABE中,∠ABE=90°,BE=15,AE=17,以AB为边作正方形ABCD,则正方形ABCD的面积等于64.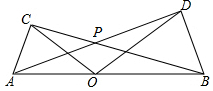 如图,点O为线段AB上的任意一点(不与A,B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC相交于点P,∠COD=110°,则∠APB=145°.
如图,点O为线段AB上的任意一点(不与A,B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC相交于点P,∠COD=110°,则∠APB=145°.