Question

5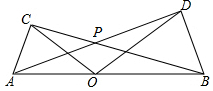．如图，点O为线段AB上的任意一点（不与A，B重合），分别以AO，BO为一腰在AB的同侧作等腰△AOC和△BOD，OA=OC，OB=OD，∠AOC与∠BOD都是锐角，且∠AOC=∠BOD，AD与BC相交于点P，∠COD=110°，则∠APB=145°．

Answer 1

分析 由∠COD=86°，∠AOC=∠BOD，求出∠AOC，根据△AOD≌△COB，得到∠OAD=∠OCB，由对顶角相等∠CMP=∠AMO，得到∠CPM=∠AOC=47°，根据邻补角求出∠APB．

解答 解：如图，∵∠AOC=∠BOD，
∴∠AOC+∠COD=∠BOD+∠COD，
∴∠AOD=∠COB，
在△AOD和△COB中，$\left\{\begin{array}{l}{OA=OC}\\{∠AOD=∠COB}\\{OD=OB}\end{array}\right.$，
∴△AOD≌△COB．
∵∠COD=86°，∠AOC=∠BOD，
∴∠AOC=∠BOD=（180°-110°）÷2=35°，
∵△AOD≌△COB，
∴∠OAD=∠OCB，
∴∠CMP=∠AMO，
∴∠CPM=∠AOC=35°，
∴∠APB=180°-∠CPM=180°-35°=145°．
故答案为：145．

点评 本题考查了全等三角形的性质与判定，解决本题的关键是证明△AOD≌△COB．