题目内容
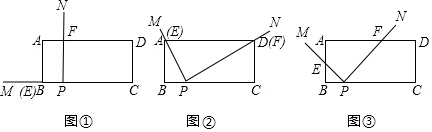
1.如图①,矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止.(1)特殊情形:如图②,发现当PM过点A时,PN也恰巧过点D,此时,△ABP∽△PCD(填“≌”或“~”);
(2)类比探究:如图③,在旋转过程中,$\frac{PE}{PF}$的值是否为定值?若是,请求出该定值;若不是,请说明理由.
分析 (1)根据有两组角对应相等的两个三角形相似,即可判定△ABP∽△PCD;
(2)过点F作FG⊥BC于G,则∠B=∠FGP,先判定△EBP∽△GPF,得出$\frac{PE}{PF}$=$\frac{PB}{FG}$,再根据$\frac{PB}{FG}$=$\frac{1}{2}$,即可得出$\frac{PE}{PF}$=$\frac{1}{2}$.
解答 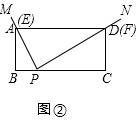 解:(1)如图②所示,∵∠MPN=90°,∠B=90°,
解:(1)如图②所示,∵∠MPN=90°,∠B=90°,
∴∠BAP+∠APB=90°=∠CPD+∠APB,
∴∠BAP=∠CPD,
又∵∠B=∠C,
∴△ABP∽△PCD;
故答案为:∽;
(2)在旋转过程中,$\frac{PE}{PF}$的值为定值.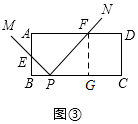
证明:如图③所示,过点F作FG⊥BC于G,则∠B=∠FGP,
∵∠MPN=90°,∠B=90°,
∴∠BEP+∠EPB=90°=∠CPF+∠EPB,
∴∠BEP=∠CPF,
∴△EBP∽△GPF,
∴$\frac{PE}{PF}$=$\frac{PB}{FG}$,
∵矩形ABGF中,FG=AB=2,而PB=1,
∴$\frac{PB}{FG}$=$\frac{1}{2}$,
∴$\frac{PE}{PF}$=$\frac{1}{2}$,
即$\frac{PE}{PF}$的值为定值$\frac{1}{2}$.
点评 本题主要考查了相似三角形的判定与性质,矩形的性质的综合应用,解决问题的关键是根据相似三角形的对应边成比例进行推导计算.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
16. 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
13. 如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )
如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )
 如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )
如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1,S2,S3三部分,则S1:S2:S3=( )| A. | 1:2:3 | B. | 1:4:9 | C. | 1:3:5 | D. | 无法确定 |
10.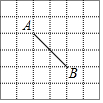 如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
 如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )| A. | 7个 | B. | 8个 | C. | 10个 | D. | 12个 |
11.计算:-3+10=( )
| A. | -13 | B. | 7 | C. | -30 | D. | -7 |
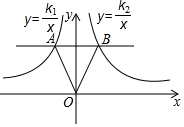 如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12.
如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12. 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.