Question

15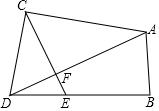．如图所示，已知：∠ACD=∠B=90°，CE⊥AD交AD于点F，交BD于点E，求证：CD²=DE•DB．

Answer 1

分析 根据如果两个三角形的两个对应角相等，那么这两个三角形相似，可以证得△DCF∽△DAC，△DEF∽△DAB；根据相似三角形的对应边成比例，即可证得．

解答 证明：∵∠DFE=∠B=90°，∠BDA=∠FDE，
∴△DEF∽△DAB，
∴DF：DB=DE：DA，
∴DE•DB=DA•DF，
∵∠DCA=∠DFC=90°，∠ADC=∠CDF，
∴△DFC∽△DCA，
∴$\frac{CD}{DF}$=$\frac{DA}{CD}$，
∴DC²=DF•DA，
又∵DF•DA=DB•DE，
∴CD²=DE•DB．

点评 本题考查了相似三角形的判定和性质，熟记掌握相似三角形的判定和性质是解题的关键．