题目内容
2. 如图所示,把长方形纸片ABCD折叠,使CD落在EF处,折痕为GH,在这个图形中,有没有关于某条直线成轴对称的两个图形呢?如果有,你能据此得到一些相等的线段和一些相等的角吗?
如图所示,把长方形纸片ABCD折叠,使CD落在EF处,折痕为GH,在这个图形中,有没有关于某条直线成轴对称的两个图形呢?如果有,你能据此得到一些相等的线段和一些相等的角吗?
分析 根据翻折变换的性质可知四边形CDGH≌四边形EFGH,进而可得出结论.
解答 解:∵把长方形纸片ABCD折叠,使CD落在EF处,折痕为GH,
∴四边形CDGH≌四边形EFGH,即四边形CDGH关于直线GH与四边形EFGH对称,
∴GD=GF,CD=EF,CH=EH,∠D=∠F,∠C=∠E,∠DGH=∠FGH,∠CHG=∠EHG.
点评 本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | a•a2=a2 | B. | (ab)2=ab2 | C. | a6÷a2=a4 | D. | (a2)3=a5 |
7.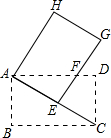 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )| A. | 2 | B. | $\frac{7}{4}$ | C. | $\frac{9}{4}$ | D. | 4 |
 如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.
如图,菱形ABCD中,两条对角线长AC=8,BD=6,则菱形ABCD的面积为24.