题目内容
13.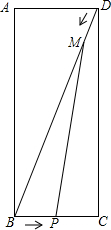 如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.
如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.
分析 根据勾股定理可得BD=13,因为DM=x,所以BM=13-x,过点M作ME⊥BC于点E,可得到△BME∽△BDC,然后根据相似三角形的性质得到$\frac{ME}{DC}=\frac{BM}{BD}$,由此即可用x表示ME,最后根据三角形的面积公式即可确定函数关系式.
解答  解:∵AB=12,BC=5,
解:∵AB=12,BC=5,
∴CD=12,
∴BD=13,
∵DM=x,
∴BM=13-x,
如图,过点M作ME⊥BC于点E,
∴ME∥DC,
∴△BME∽△BDC,
∴$\frac{ME}{DC}=\frac{BM}{BD}$,
∴ME=12-$\frac{12}{13}$x,
∵S△MBP=$\frac{1}{2}$×BP×ME,
∴y=-$\frac{6}{13}$x2+6x,P不与B重合,那么x>0,可与点C重合,那么x≤6.
∴y与x之间的函数关系式:y=-$\frac{6}{13}$x2+6x(0<x≤5).
点评 此题主要考查了动点问题的函数图象,相似三角形的性质和判定,求函数关系式.本题的难点是利用相似得到△MBP中BP边上的高ME的代数式,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.在△ABC中,∠C=90°,sinA=$\frac{3}{5}$,则sinB的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{\sqrt{21}}{5}$ |
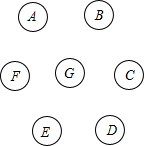 如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件:
如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件: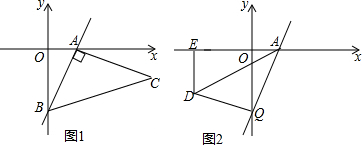
 如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s.
如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s. 已知线段AB上有C、D两点,AD=35,BC=45,AC=$\frac{3}{5}$BD.求AB的长.
已知线段AB上有C、D两点,AD=35,BC=45,AC=$\frac{3}{5}$BD.求AB的长.