题目内容
2.先化简($\frac{x-1}{x}$-$\frac{x-2}{x+1}$)÷$\frac{4{x}^{2}-2x}{{x}^{2}+2x+1}$,然后从-1≤x≤1的范围内选取一个合适的整数作为x的值代入求值.分析 根据分式的运算法则即可化简,然后根据根式有意义的条件即可求出该分式的值.
解答 解:原式=$\frac{(x-1)(x+1)-x(x-2)}{x(x+1)}$÷$\frac{2x(2x-1)}{(x+1)^{2}}$
=$\frac{2x-1}{x(x+1)}•\frac{(x+1)^{2}}{2x(2x-1)}$
=$\frac{x+1}{2{x}^{2}}$
∵x≠0,-1,$\frac{1}{2}$
-1≤x≤1
∴x=1
∴原式=$\frac{1+1}{2×{1}^{2}}$=1
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
10.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{17}$ | B. | $\sqrt{12}$ | C. | $\sqrt{2.4}$ | D. | $\sqrt{\frac{1}{3}}$ |
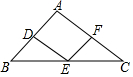 如图,△ABC的边AB、BC、CA的中点分别是D、E、F,已知AB=8,AC=10,则四边形ADEF的周长是( )
如图,△ABC的边AB、BC、CA的中点分别是D、E、F,已知AB=8,AC=10,则四边形ADEF的周长是( )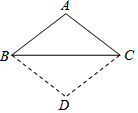 如图,已知△ABC,AB=AC,将△ABC沿边BC翻折,得到的△DBC与原△ABC拼成四边形ABDC.求证:四边形ABDC是菱形.
如图,已知△ABC,AB=AC,将△ABC沿边BC翻折,得到的△DBC与原△ABC拼成四边形ABDC.求证:四边形ABDC是菱形.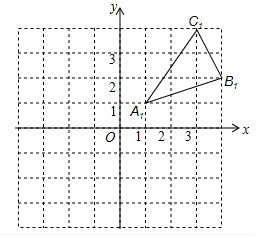 如图,△A1B1C1是△ABC向上平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
如图,△A1B1C1是△ABC向上平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).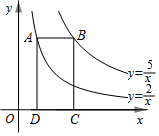 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{5}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD是矩形,则它的面积为3.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{5}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD是矩形,则它的面积为3.