题目内容
6.计算:(1)($\frac{3x}{x-2}$-$\frac{x}{x+2}$)•$\frac{{x}^{2}-4}{x}$(请用两种方法解答)
(2)($\frac{1}{a}$+$\frac{1}{b}$)2÷($\frac{1}{{a}^{2}}$-$\frac{1}{{b}^{2}}$)(请用两种方法解答)
(3)($\frac{x}{x+y}$+$\frac{2y}{x+y}$)•$\frac{xy}{x+2y}$÷($\frac{1}{x}$+$\frac{1}{y}$)
(4)($\frac{a+b}{a-b}$)2•$\frac{2a-2b}{a+b}$-$\frac{a}{a-b}$$÷\frac{a}{2b}$.
分析 (1)法1:原式括号中通分并利用同分母分式的减法法则计算,约分即可得到结果;法2:原式利用乘法分配律计算即可得到结果;
(2)法1:原式先计算乘方运算,以及括号中的运算,再计算除法运算即可得到结果;法2:原式除数利用平方差公式化简,约分后计算即可得到结果;
(3)原式括号中两项通分并利用同分母分式的加法法则计算,约分即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)法1:原式=$\frac{3{x}^{2}+6x-{x}^{2}+2x}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{x}$=2x+8;
法2:原式=$\frac{3x}{x-2}$•$\frac{(x+2)(x-2)}{x}$-$\frac{x}{x+2}$•$\frac{(x+2)(x-2)}{x}$=3(x+2)-x+2=3x+6-x+2=2x+8;
(2)法1:原式=$\frac{(a+b)^{2}}{{a}^{2}{b}^{2}}$•$\frac{{a}^{2}{b}^{2}}{(b+a)(b-a)}$=$\frac{b+a}{b-a}$;
法2:原式=($\frac{1}{a}$+$\frac{1}{b}$)2÷($\frac{1}{a}$+$\frac{1}{b}$)($\frac{1}{a}$-$\frac{1}{b}$)=$\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{a}-\frac{1}{b}}$=$\frac{a+b}{b-a}$;
(3)原式=$\frac{x+2y}{x+y}$•$\frac{xy}{x+2y}$•$\frac{xy}{x+y}$=$\frac{{x}^{2}{y}^{2}}{(x+y)^{2}}$;
(4)原式=$\frac{(a+b)^{2}}{(a-b)^{2}}$•$\frac{2(a-b)}{a+b}$-$\frac{a}{a-b}$•$\frac{2b}{a}$=$\frac{2(a+b)}{a-b}$-$\frac{2b}{a-b}$=$\frac{2a+2b-2b}{a-b}$=$\frac{2a}{a-b}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案(1)请填写表格;(单位:吨)
| C | D | 总计 | |
| A | x吨 | 200-x | 200吨 |
| B | 240-x | x+60 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
(3)当x=100时,试求A,B两村运往两仓库的柑橘的运输总费用.
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
 如图为小李家住房的结构,小李打算把卧室和客厅铺上地板,请你帮助他算一算,他至少应买木地板多少?
如图为小李家住房的结构,小李打算把卧室和客厅铺上地板,请你帮助他算一算,他至少应买木地板多少? 如图,边长为a、2的两个正方形拼在一起,试写出阴影部分的面积,并求出当a=4cm时阴影部分的面积.
如图,边长为a、2的两个正方形拼在一起,试写出阴影部分的面积,并求出当a=4cm时阴影部分的面积.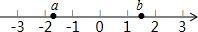 实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$. 在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求证:AB2=BD•BC.
在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求证:AB2=BD•BC.