题目内容
14．
如图，通过计算大正方形的面积，可以验证的公式是（ ）| A． | （a+b+c）2=a2+b2+c2 | B． | （a+b+c）2=a2+b2+c2+ab+bc+ac | ||
| C． | （a+b+c）2=a2+b2+c2+2ab+2bc+2ac | D． | （a+b+c）2=a2+b2+c2+2ab+3bc+4ac |
分析 直接利用图形面积得出等式进而得出答案．
解答 解：如图所示：（a+b+c）2=a2+b2+c2+2ab+2bc+2ac，
故选：C．
点评 此题主要考查了完全平方公式的几何背景，正确表示出各部分面积是解题关键．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
4．已知|2x+3|=-2x-3，则x的取值范围是（ ）
| A． | x＞-$\frac{3}{2}$ | B． | x＜-$\frac{3}{2}$ | C． | x≥-$\frac{3}{2}$ | D． | x≤-$\frac{3}{2}$ |
5．直线 y=x-1与坐标轴交于A、B两点，点C在x轴上，若△ABC为等腰三角形且S△ABC=$\frac{\sqrt{2}}{2}$，则点C的坐标为（ ）
| A． | 、（0，0 ） | B． | （1-$\sqrt{2}$，0）或（$\sqrt{2}+$1，0） | C． | 、（$\sqrt{2}$+1，0 ） | D． | 、（-$\sqrt{2}$-1，0）或（-$\sqrt{2}$+1，0） |
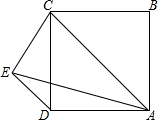在正方形ABCD中，AC为对角线，DE平行于AC，AE=AC，求∠CED的度数．