题目内容
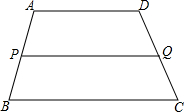 如图,在梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
如图,在梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.(1)线段PQ与BC平行吗?为什么?
(2)测量并回答:DQ与CQ是否相等?
(3)通过测量并判断:
| 1 |
| 2 |
考点:梯形中位线定理
专题:
分析:(1)根据平行线的传递性可得出答案;
(2)先测量,再根据平行线分线段成比例定理证明即可;
(3)先测量,再根据梯形中位线定理即可得出
(AD+BC)=PQ成立.
(2)先测量,再根据平行线分线段成比例定理证明即可;
(3)先测量,再根据梯形中位线定理即可得出
| 1 |
| 2 |
解答:解:(1)PQ∥BC,理由如下:
∵PQ∥AD,
又∵AD∥BC,
∴PQ∥BC(平行于同一直线的两直线平行);
(2)通过测量,可得出DQ=CQ.理由如下:
∵PQ∥AD∥BC,
∴AP:PB=DQ:QC,
∵AP=BP,
∴DQ=CQ;
(3)通过测量,可得出
(AD+BC)=PQ.理由如下:
∵在梯形ABCD中,AD∥BC,AP=BP,DQ=CQ,
∴PQ是梯形ABCD的中位线,
∴
(AD+BC)=PQ.
∵PQ∥AD,
又∵AD∥BC,
∴PQ∥BC(平行于同一直线的两直线平行);
(2)通过测量,可得出DQ=CQ.理由如下:
∵PQ∥AD∥BC,
∴AP:PB=DQ:QC,
∵AP=BP,
∴DQ=CQ;
(3)通过测量,可得出
| 1 |
| 2 |
∵在梯形ABCD中,AD∥BC,AP=BP,DQ=CQ,
∴PQ是梯形ABCD的中位线,
∴
| 1 |
| 2 |
点评:本题考查了梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.也考查了平行线的性质以及平行线分线段成比例定理.

练习册系列答案
相关题目
 △ABC中,BF、CF是角平分线,∠A=70°,则∠BFC=( )
△ABC中,BF、CF是角平分线,∠A=70°,则∠BFC=( )| A、125° | B、110° |
| C、100° | D、150° |
已知x=3是关于x的方程ax+2x-3=0的解,则a的值为( )
| A、-1 | B、-2 | C、-3 | D、1 |
 如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数.
如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数.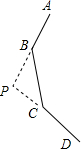 如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.
如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n. 用尺规作图:
用尺规作图: 如图,在△ABC中,AB=12,AC=18,AD是∠BAC的平分线,过点B作AD的垂线,交AD于D,M是BC的中点,求MD的长.
如图,在△ABC中,AB=12,AC=18,AD是∠BAC的平分线,过点B作AD的垂线,交AD于D,M是BC的中点,求MD的长.