题目内容
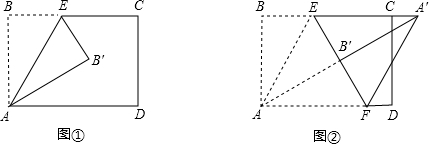
7.有一张长方形纸片ABCD,按下面步骤进行折叠:第一步:如图①,点E在边BC上,沿AE折叠,点B落在点B′处;
第二步:如图②,沿EB′折叠,使点A落在BC延长线上的点A′处,折痕为EF.
有下列结论:①△AEF是等边三角形;②EF垂直平分AA′;③CA′=FD.( )
| A. | 只有②正确 | B. | 只有①②正确 | C. | 只有①③正确 | D. | ①②③都正确 |
分析 ①正确.只要证明∠AEF=∠EAF=∠EFA=60°,即可推出△AEF是等边三角形.
②正确.只要证明四边形AEA′F是菱形即可.
③错误.AB、BC的长度不确定,无法判断AC与DF的大小关系.
解答 解:∵∠BEA=∠AEF=∠A′EF,又∠BEA+∠AEF+∠A′EF=180°,
∴∠BEA=∠AEF=∠A′EF=60°,
∵BC∥AD,
∴∠BEA=∠EAF=60°,
∴∠AEF=∠EAF=∠EFA=60°,
∴△AEF是等边三角形,故①正确,
∴△EFA′是等边三角形,
∴AE=EA′=A′F=AF,
∴四边形AEA′F是菱形,
∴EF垂直平分AA′,故②正确,
由于AB、BC的长度不确定,所以AC不一定等于DF,故③错误,
故选B.
点评 本题考查翻折变换、线段的垂直平分线的性质、等边三角形的判定和性质、矩形的性质、菱形的判定和性质等知识,解题的关键是灵活运用所学知识,属于基础题,中考常考题型.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.三角形两边长为4和11,第三边长为3-6m,则m的取值范围是( )
| A. | -2<m<-$\frac{2}{3}$ | B. | m>-2 | C. | -2≤m≤-$\frac{2}{3}$ | D. | m<-2 |
19.某中学要组织一次篮球比赛,赛制为单循环形式(毎两队之间都赛一场),计划安排21场比赛,求参加的球队支数,如果设参加的球队支数为x,则可列方程为( )
| A. | $\frac{1}{2}$x(x+1)=21 | B. | x(x+1)=21 | C. | $\frac{1}{2}$x(x-1)=21 | D. | x(x-1)=21 |
16.一份稿件,甲8小时打完,乙6小时打完,则乙的工作效率比甲快百分之几?下面列式正确的是( )
| A. | (8-6)÷8 | B. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{6}$ | C. | $\frac{1}{6}$÷$\frac{1}{8}$ | D. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{8}$ |
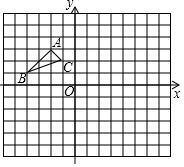 如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2).
如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2). 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉子是学.
如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉子是学.