题目内容
已知△ABC中，∠C=90°，∠A=40°，CD是AB边上的高，CE是∠BCA的角平分线，分别交AB于点D、E．求∠ECD的度数．考点：三角形内角和定理
专题：
分析：根据直角三角形两锐角互余求出∠ACD，再根据角平分线的定义求出∠ACE，然后根据∠DCE=∠ACD-∠ACE计算即可得解．
解答：解：∵∠C=90°，CD是AB边上的高，∠A=40°，
∴∠ACD=50°，
又∵CE是∠BCA的角平分线，
∴∠ACE=45°，
∴∠DCE=∠ACD-∠ACE=50°-45°=5°．
∴∠ACD=50°，
又∵CE是∠BCA的角平分线，
∴∠ACE=45°，
∴∠DCE=∠ACD-∠ACE=50°-45°=5°．
点评：本题考查了三角形的内角和定理，角平分线的定义，准确识图，理清图中各角度之间的关系是解题的关键．
练习册系列答案
相关题目
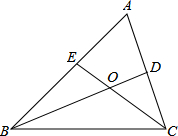如图，∠A=60°，BD、CE是△ABC的角平分线，求证：BC=BE+CD．
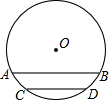如图，AB、CD都是⊙O的弦，且AB∥CD．求证：AC=BD．