题目内容
 如图所示,在Rt△ABC中,∠BAC=90°,点D,E在BC上,且BE=AB,CD=AC,求∠DAE的度数.
如图所示,在Rt△ABC中,∠BAC=90°,点D,E在BC上,且BE=AB,CD=AC,求∠DAE的度数.考点:等腰三角形的性质
专题:
分析:根据等边对等角的性质求出∴∠BEA=∠BAE,∠CDA=∠CAD,设∠BEA=∠BAE=x,∠CDA=∠CAD=y,∠EAD=z,再根据三角形的内角和定理和直角的定义求出∠DAE的度数.
解答:解:∵BE=AB,CD=AC,
∴∠BEA=∠BAE,∠CDA=∠CAD,
设∠BEA=∠BAE=x,∠CDA=∠CAD=y,∠EAD=z,
∴在△AED中,x+y+z=180①,
∵∠BAC=90°,
∴x+y-z=90②,
①+②得:x+y=135,
∴z=45,
∴∠DAE的度数是45°.
∴∠BEA=∠BAE,∠CDA=∠CAD,
设∠BEA=∠BAE=x,∠CDA=∠CAD=y,∠EAD=z,
∴在△AED中,x+y+z=180①,
∵∠BAC=90°,
∴x+y-z=90②,
①+②得:x+y=135,
∴z=45,
∴∠DAE的度数是45°.
点评:本题考查了等腰三角形的性质,解题的关键是利用等腰三角形的等边对等角的性质得到相等的角,难度不大.

练习册系列答案
相关题目

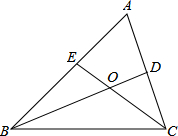 如图,∠A=60°,BD、CE是△ABC的角平分线,求证:BC=BE+CD.
如图,∠A=60°,BD、CE是△ABC的角平分线,求证:BC=BE+CD.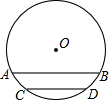 如图,AB、CD都是⊙O的弦,且AB∥CD.求证:AC=BD.
如图,AB、CD都是⊙O的弦,且AB∥CD.求证:AC=BD.