题目内容
如图，在△ABC中，CD⊥AB于D，且AC=4cm，BC=3cm，AB=5cm，指出图中各对相似三角形及其相似比．考点：相似三角形的判定
专题：计算题
分析：先利用勾股定理的逆定理证明△ABC为直角三角形，∠ACB=90°，再由CD⊥AB得到∠ADC=∠CDB=90°，然后根据有两组角对应相等的两个三角形相似证明
Rt△ABC∽Rt△ACD，Rt△BAC∽Rt△BCD，则Rt△ACD∽Rt△CBD，再利用相似比的定义分别计算各对相似三角形的相似比．
Rt△ABC∽Rt△ACD，Rt△BAC∽Rt△BCD，则Rt△ACD∽Rt△CBD，再利用相似比的定义分别计算各对相似三角形的相似比．
解答：解：∵32+42=52，
∴BC2+AC2=AB2，
∴△ABC为直角三角形，∠ACB=90°，
∵CD⊥AB，
∴∠ADC=∠CDB=90°，
∵∠CAB=∠DAC，
∴Rt△ABC∽Rt△ACD，相似比=
=
；
∵∠CBD=∠ABC，
∴Rt△BAC∽Rt△BCD，相似比=
=
；
∴Rt△ACD∽Rt△CBD，相似比=
=
．
∴BC2+AC2=AB2，
∴△ABC为直角三角形，∠ACB=90°，
∵CD⊥AB，
∴∠ADC=∠CDB=90°，
∵∠CAB=∠DAC，
∴Rt△ABC∽Rt△ACD，相似比=
| AB |
| AC |
| 5 |
| 4 |
∵∠CBD=∠ABC，
∴Rt△BAC∽Rt△BCD，相似比=
| AB |
| BC |
| 5 |
| 3 |
∴Rt△ACD∽Rt△CBD，相似比=
| AC |
| CB |
| 4 |
| 3 |
点评：本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似．也考查了勾股定理的逆定理．
练习册系列答案
相关题目
关于x的一元二次方程（a-c）x2+bx+
=0有两个相等的实数根，那么以a、b、c为三边长的三角形是（ ）
| a+c |
| 4 |
| A、以a为斜边的直角三角形 |
| B、以c为斜边的直角三角形 |
| C、以b为底边的等腰三角形 |
| D、以c为底边的等腰三角形 |
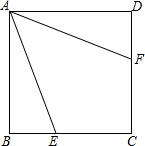如图所示，正方形ABCD中，E是BC边上的点，F是CD边上的点，且AE=AF，AB=4，设△AEF面积为y，EC为x．求y与x之间函数关系并画出这个函数图象．
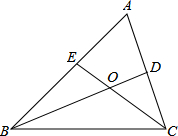如图，∠A=60°，BD、CE是△ABC的角平分线，求证：BC=BE+CD．