题目内容
6.化简:(1)$\sqrt{8}$-$\sqrt{2}$+$\sqrt{32}$
(2)$\sqrt{12}$+6$\sqrt{\frac{1}{3}}$-$\sqrt{27}$
(3)($\sqrt{5}$-$\sqrt{7}$)($\sqrt{5}$+$\sqrt{7}$)+2
(4)$\frac{\sqrt{20}+\sqrt{15}}{\sqrt{5}}$-2÷$\frac{4}{3}$$\sqrt{3}$
(5)${({π-1})^0}+{({\frac{{\sqrt{3}}}{2}})^{-1}}+|{5-\sqrt{27}}|-\sqrt{{{10}^2}-{6^2}}$
(6)${({2\sqrt{2}+3})^{2011}}{({2\sqrt{2}-3})^{2012}}-4\sqrt{\frac{1}{8}}-\sqrt{{{(1-\sqrt{2})}^2}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用平方差公式计算;
(4)根据二次根式的除法法则运算;
(5)根据零指数幂和负整数指数幂的意义计算;
(6)利用积的乘方和二次根式的性质得到原式=[(2$\sqrt{2}$+3)(2$\sqrt{2}$-3)]2011•(2$\sqrt{2}$-3)-$\sqrt{2}$-($\sqrt{2}$-1),然后利用平方差公式计算.
解答 解:(1)原式=2$\sqrt{2}$-$\sqrt{2}$+4$\sqrt{2}$
=5$\sqrt{2}$;
(2)原式=2$\sqrt{3}$+2$\sqrt{3}$-3$\sqrt{3}$
=$\sqrt{3}$;
(3)原式=5-7+2
=0;
(4)原式=$\sqrt{\frac{20}{5}}$+$\sqrt{\frac{15}{5}}$-2×$\frac{\sqrt{3}}{4}$
=2+$\sqrt{3}$-$\frac{\sqrt{3}}{2}$
=2+$\frac{\sqrt{3}}{2}$;
(5)原式=1+$\frac{2}{\sqrt{3}}$+3$\sqrt{3}$-5-$\sqrt{{8}^{2}}$
=1+$\frac{2\sqrt{3}}{3}$+3$\sqrt{3}$-5-8
=$\frac{11\sqrt{3}}{3}$-12;
(6)原式=[(2$\sqrt{2}$+3)(2$\sqrt{2}$-3)]2011•(2$\sqrt{2}$-3)-$\sqrt{2}$-($\sqrt{2}$-1)
=(8-9)2011•(2$\sqrt{2}$-3)-$\sqrt{2}$-($\sqrt{2}$-1)
=-2$\sqrt{2}$+3-$\sqrt{2}$-$\sqrt{2}$+1
=-4$\sqrt{2}$+4.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了零指数幂和负整数指数幂.

 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案| A. | 晴天的早晨,太阳从东方升起 | |
| B. | 测量某天的最低气温,结果为-150℃ | |
| C. | 打开数学课本时刚好翻到第60页 | |
| D. | 在一次体育考试中,小王跑100米用了4秒钟 |
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
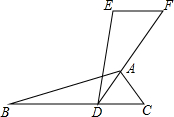 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )| A. | 50° | B. | 60° | C. | 100° | D. | 120° |
 如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为$\frac{4}{5}$.
如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为$\frac{4}{5}$.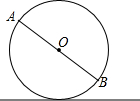 如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.
如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.