题目内容
14.已知三角形ABC的三个顶点坐标分别为A(0,0),B(4,-2),C(5,3),则三角形ABC的面积为11.分析 根据题意可以画出相应的图形,然后根据A(0,0),B(4,-2),C(5,3),可以求得矩形EFCD面积、三角形AEB的面积、三角形BFC的面积、三角形ACD的面积,从而可以求得三角形ABC的面积.
解答 解:如下图所示: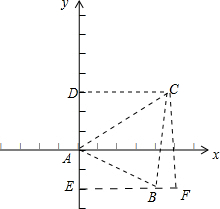
过点C作CD⊥y轴于点D,过点B作BE⊥y轴于点E,过点C作CF⊥x轴交EB的延长线于点F,
∵A(0,0),B(4,-2),C(5,3),
∴S△ABC=S矩形EFCD-S△AEB-S△BFC-S△CAD
=5×[3-(-2)]-$\frac{4×|-2|}{2}$-$\frac{(5-4)×5}{2}-\frac{3×5}{2}$
=25-4-$\frac{5}{2}$$-\frac{15}{2}$
=11.
故答案为:11.
点评 本题考查坐标与图形的性质、三角形的面积,解题的关键是运用转化的数学思想,将所求问题转化为求其它图形的面积,进而得到所求问题的答案.

练习册系列答案
相关题目
2.下列各式正确的是( )
| A. | $\sqrt{(-4)×(-25)}$=$\sqrt{-4}$×$\sqrt{-25}$=10 | B. | $\sqrt{{2^2}+{3^2}}$=2+3=5 | ||
| C. | $\sqrt{\frac{2}{3}}$=$\frac{1}{3}$$\sqrt{6}$ | D. | $\frac{{-\sqrt{45}}}{{\sqrt{5}}}=\sqrt{\frac{-45}{5}}$ |
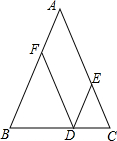 如图,在△ABC中,AB=AC,点D在边BC上,过点D作DE∥AB与边AC交于点E、DF∥AC与边AB交于点F.
如图,在△ABC中,AB=AC,点D在边BC上,过点D作DE∥AB与边AC交于点E、DF∥AC与边AB交于点F. 实数a,b,c在数轴上的对应关系如图,化简下面的式子:|a-b|-|c-a|+|b-c|+|a|.
实数a,b,c在数轴上的对应关系如图,化简下面的式子:|a-b|-|c-a|+|b-c|+|a|.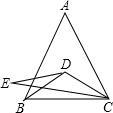 如图,在△ABC中,AB=AC,∠A=50°,D为△ABC内一点,连接BD,CD,E为△ABC外一点,连接CE,DE,已知BD=CD,E=AB,CD平分∠ECA.
如图,在△ABC中,AB=AC,∠A=50°,D为△ABC内一点,连接BD,CD,E为△ABC外一点,连接CE,DE,已知BD=CD,E=AB,CD平分∠ECA.