题目内容
20.观察下列各式的规律:1×2×3×4+1=(1×4+1)2;2×3×4×5+1=(2×5+1)2;3×4×5×6+1=(3×6+1)2;…
①写出第五个式子5×6×7×8+1=(5×8+1)2;
②写出第n个式子,并用所学知识说明理由.
分析 ①仿照给定等式继续写下去,即可得出结论;
②找出给定算式的变化规律,根据规律写出第n个式子,再将等式右边项进行分解因式去与左边相比较,即可证出结论.
解答 解:①比着给定算式写下去:4×5×6×7+1=(4×7+1)2;5×6×7×8+1=(5×8+1)2;…
故答案为:5×6×7×8+1=(5×8+1)2.
②观察给定等式,可发现等号前面四个相乘的因式为连续的自然数,等号后面口号内两因式为前面四因数的首项和尾项.
按照规律可知:第n个式子为n×(n+1)×(n+2)×(n+3)+1=[n×(n+3)+1]2,
证明:∵右边=[n×(n+3)+1]2=[n×(n+3)]2+2n×(n+3)+1=n×(n+3)×[n×(n+3)+2]+1=n×(n+3)×(n2+3n+2)+1=n×(n+1)×(n+2)×(n+3)+1=左边,
∴等式成立.
故结论成立.
点评 本题考查了数的变化规律以及利用完全平方法和十字相乘法分解因式,解题的关键是:①仿照例子写下去;②找出规律得出结论.本题属于中档题,①只需仿照例子写下去即可,②需找到变化的规律,结合规律找出第n个式子,再通过分解因式的方法去证明结论.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
10.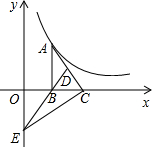 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线$y=\frac{k}{x}({x>0})$的图象经过点A,若S△BEC=3,则k等于( )
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线$y=\frac{k}{x}({x>0})$的图象经过点A,若S△BEC=3,则k等于( )
 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线$y=\frac{k}{x}({x>0})$的图象经过点A,若S△BEC=3,则k等于( )
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线$y=\frac{k}{x}({x>0})$的图象经过点A,若S△BEC=3,则k等于( )| A. | 12 | B. | 6 | C. | 3 | D. | 2 |
20.下列条件中,不能判定四边形ABCD为平行四边形的条件是( )
| A. | AB=AD,BC=CD | B. | ∠A=∠C,∠B=∠D | C. | AB∥CD,AB=CD | D. | AB=CD,AD=BC |
 如图,已知?ABCD中,AB=6,∠DAB=60°,AC平分∠DAB,E为AB的中点,点F是AC上一动点,求EF+BF的最小值.
如图,已知?ABCD中,AB=6,∠DAB=60°,AC平分∠DAB,E为AB的中点,点F是AC上一动点,求EF+BF的最小值.