题目内容
2.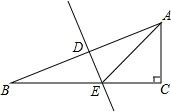 在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.(1)若∠CAE=∠B+30°,求∠B的度数;
(2)若∠B=15°,AC=a,AB=b,求DE的长(用含a、b的代数式表示).
分析 (1)由DE是斜边AB的垂直平分线,可得AE=BE,即可证得∠BAE=∠B,然后由∠CAE=∠B+30°,可得∠B+∠B+∠B+30°=90°,继而求得答案;
(2)由∠B=15°,可求得∠AEC的度数,继而可求得AE的长,然后由勾股定理求得DE的长.
解答 解:(1)∵DE是斜边AB的垂直平分线,
∴AE=BE,
∴∠BAE=∠B,
∵∠CAE=∠B+30°,∠C=90°,
∴∠B+∠BAE+∠CAE=90°,
∴∠B+∠B+∠B+30°=90°,
解得:∠B=20°;
(2)∵∠B=15°,
∴∠AEC=∠B+∠BAE=2∠B=30°,
∵∠C=90°,AC=a,
∴AE=2AC=2a,
∵DE是斜边AB的垂直平分线,AB=b,
∴∠ADE=90°,AD=$\frac{1}{2}$AB=$\frac{1}{2}$b,
∴DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=$\sqrt{4{a}^{2}-\frac{1}{4}{b}^{2}}$=$\frac{\sqrt{16{a}^{2}-{b}^{2}}}{2}$.
点评 此题考查了线段垂直平分线的性质、直角三角形的性质以及勾股定理.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
13.同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
10.下列长度的三条线段,能组成三角形的是( )
| A. | 1,2,3 | B. | 10,5,4 | C. | 5,2,6 | D. | 2,4,8 |

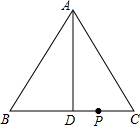 如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( )
如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( ) 如图,△ABC≌△DCB,∠DBC=40°,则∠AEB=80度.
如图,△ABC≌△DCB,∠DBC=40°,则∠AEB=80度.