题目内容
17.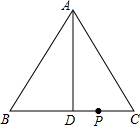 如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( )
如图,在△ABC中,AB=AC,AD⊥BC于点D,AB=5,AD=4,点P是BC边上的一动点,且不与B、C重合,则点P到AB、AC的距离之和为( )| A. | 4.8 | B. | 3 | C. | 2.4 | D. | 不确定 |
分析 过点P作PF⊥AC,PE⊥AB,连接AP,根据三角形ABC的面积为的值即可求出PF+PE的长.
解答 解:过点P作PF⊥AC,PE⊥AB,连接AP,
∵AD⊥BC于点D,AB=5,AD=4,
∴BD=3,
∴AB=AC,
∴BD=BD=6,
∴S△ABC=$\frac{1}{2}$AD•BC=12,
∵S△ABP+S△APC=S△ABC,
∴$\frac{1}{2}$AB•PF+$\frac{1}{2}$ACP•PF=12,
∴PE+PF=4.8,
故选A.
点评 本题考查了等腰三角形的性质、勾股定理的运用、三角形面积公式的运用,解题的关键是作出高线,把PE+PF作为一个整体求出.

练习册系列答案
相关题目
12. 如图,在△ABC中,点D在CB的延长线上,∠A=70°,∠ABD=120°,则∠C等于( )
如图,在△ABC中,点D在CB的延长线上,∠A=70°,∠ABD=120°,则∠C等于( )
 如图,在△ABC中,点D在CB的延长线上,∠A=70°,∠ABD=120°,则∠C等于( )
如图,在△ABC中,点D在CB的延长线上,∠A=70°,∠ABD=120°,则∠C等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
2.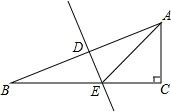 在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
(1)若∠CAE=∠B+30°,求∠B的度数;
(2)若∠B=15°,AC=a,AB=b,求DE的长(用含a、b的代数式表示).
 在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.(1)若∠CAE=∠B+30°,求∠B的度数;
(2)若∠B=15°,AC=a,AB=b,求DE的长(用含a、b的代数式表示).
9.下列说法正确的是( )
| A. | 单项式a的系数是0 | |
| B. | 单项式-$\frac{3xy}{5}$的系数和次数分别是-3和2 | |
| C. | 3mn与4nm不是同类项 | |
| D. | 单项式-3πxy2z3的系数和次数分别是-3π和6 |
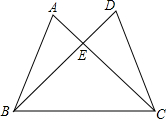 如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.
如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.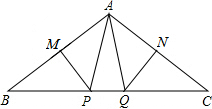 如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.
如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.