题目内容
12.如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②求证:BD=2EC;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.

分析 (1)①根据等腰直角三角形的性质得出∠CBA=45°,再利用角平分线的定义解答即可;
②延长CE交BA的延长线于点G得出CE=GE,再利用AAS证明△ABD≌△ACG,利用全等三角形的性质解答即可;
(2)过点A作AH⊥AE,交BE于点H,证明△ABH≌△ACE,进而得出CE=BH,利用等腰直角三角形的判定和性质解答即可.
解答 解:(1)①∵在△ABC中,∠BAC=90°,AB=AC,
∴∠CBA=45°,
∵BD平分∠ABC,
∴∠DBA=22.5°,
∵CE⊥BD,
∴∠ECD+∠CDE=90°,∠DBA+∠BDA=90°,
∵∠CDE=∠BDA,
∴∠ECD=∠DBA=22.5°;
②延长CE交BA的延长线于点G,如图1:
∵BD平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD与△ACG中,
$\left\{\begin{array}{l}{∠DBA=∠ACG}\\{∠BAC=∠CAG}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)结论:BE-CE=2AF.
过点A作AH⊥AE,交BE于点H,如图2: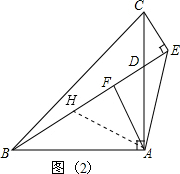
∵AH⊥AE,
∴∠BAH+∠HAC=∠HAC+∠CAE,
∴∠BAH=∠CAE,
在△ABH与△ACE中,
$\left\{\begin{array}{l}{∠HBA=∠ECA}\\{AB=AC}\\{∠BAH=∠ACE}\end{array}\right.$,
∴△ABH≌△ACE(ASA),
∴CE=BH,AH=AE,
∴△AEH是等腰直角三角形,
∴AF=EF=HF,
∴BE-CE=2AF.
点评 本题考查的是全等三角形的判定和性质,正确的构建出与所求和已知相关的全等三角形,是解答本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
2.下列说法中正确的是( )
| A. | |-a|是正数 | B. | $\sqrt{2}$是正分数 | ||
| C. | 若|-a|=-a,则a是非正数 | D. | -x2y与2xy2是同类项 |
4.已知|x+2|+(y-3)2=0,则xy的值为( )
| A. | -6 | B. | 6 | C. | -8 | D. | 8 |
1.用一条长为60cm的绳子围成一个面积为acm2的长方形,a的值不可能为( )
| A. | 240 | B. | 225 | C. | 60 | D. | 30 |
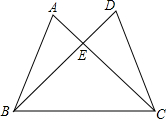 如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.
如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.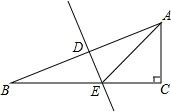 在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.