题目内容
13.同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 首先利用列举法可得:同时抛掷两枚质地均匀的硬币,等可能的结果有:正正,正反,反正,反反;然后直接利用概率公式求解即可求得答案.
解答 解:∵同时抛掷两枚质地均匀的硬币,等可能的结果有:正正,正反,反正,反反;
∴出现两个正面朝上的概率是:$\frac{1}{4}$.
故选D.
点评 此题考查了列举法求概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
4.已知|x+2|+(y-3)2=0,则xy的值为( )
| A. | -6 | B. | 6 | C. | -8 | D. | 8 |
1.用一条长为60cm的绳子围成一个面积为acm2的长方形,a的值不可能为( )
| A. | 240 | B. | 225 | C. | 60 | D. | 30 |
18.下列分式中,一定有意义的是( )
| A. | $\frac{x-3}{{x}^{2}-4}$ | B. | $\frac{y-1}{{y}^{2}+1}$ | C. | $\frac{{x}^{2}+1}{3x}$ | D. | $\frac{x-1}{x+1}$ |
2.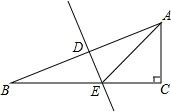 在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
(1)若∠CAE=∠B+30°,求∠B的度数;
(2)若∠B=15°,AC=a,AB=b,求DE的长(用含a、b的代数式表示).
 在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.
在Rt△ABC中,斜边AB的垂直平分线DE,分别交AB、BC于D、E.(1)若∠CAE=∠B+30°,求∠B的度数;
(2)若∠B=15°,AC=a,AB=b,求DE的长(用含a、b的代数式表示).
3.判断下列变量之间的关系是不是函数关系,是的画“√”,不是的画“×”,并在横线上写出理由.
(1)高线长h的等腰三角形的底边长a与面积S.( )√;
(2)关系式y=±$\sqrt{x}$中的y与x.( )×.
(3)下表中的v与s.( )√.
(4)关系式y=x2中的y与x.( )×.
(1)高线长h的等腰三角形的底边长a与面积S.( )√;
(2)关系式y=±$\sqrt{x}$中的y与x.( )×.
(3)下表中的v与s.( )√.
| 助跑速度v(m/s) | 7.5 | 8 | 8.5 |
| 跳远的距离s(m) | 4.78 | 5.44 | 6.14 |
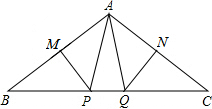 如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.
如图所示,∠BAC=120°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.