题目内容
7．
如图，△ABC≌△DCB，∠DBC=40°，则∠AEB=80度．
分析 根据全等三角形的性质求出∠ACB，根据三角形的外角性质得出∠AEB=∠ACB+∠DBC，代入求出即可．
解答 解：∵△ABC≌△DCB，∠DBC=40°，
∴∠ACB=∠DBC=40°，
∴∠AEB=∠ACB+∠DBC=40°+40°=80°，
故答案为：80．
点评 本题考查了三角形的外角性质，全等三角形的性质的应用，能根据全等三角形的性质求出∠ACB的度数是解此题的关键，注意：全等三角形的对应角相等，对应边相等．
练习册系列答案
相关题目
18．下列分式中，一定有意义的是（ ）
| A． | $\frac{x-3}{{x}^{2}-4}$ | B． | $\frac{y-1}{{y}^{2}+1}$ | C． | $\frac{{x}^{2}+1}{3x}$ | D． | $\frac{x-1}{x+1}$ |
15．已知点P（m，2）与Q（3，n）关于y轴对称，则（m+n）2015的值为（ ）
| A． | -1 | B． | 1 | C． | 52015 | D． | -52015 |
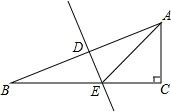在Rt△ABC中，斜边AB的垂直平分线DE，分别交AB、BC于D、E．
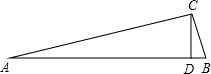已知：如图，在Rt△ABC中，∠C=90°，∠B=5∠A，CD⊥AB，垂足为D，求证：AB=4CD．（提示．作斜边AB上的中线CM）