题目内容
11．一个单项式与-24xn-1yn-1z2的积为48xnyn+1z2，求这个单项式．并求出当x=$\frac{1}{2}$，y=4，z=2015时此单项式的值．分析 利用单项式除法得出所求单项式，进而将已知数据代入求出答案．
解答 解：∵一个单项式与-24xn-1yn-1z2的积为48xnyn+1z2，
∴这个单项式为：48xnyn+1z2÷（-24xn-1yn-1z2）=-2xy2，
当x=$\frac{1}{2}$，y=4，z=2015时，
原式=-2xy2=-2×$\frac{1}{2}$×42=-16．
点评 此题主要考查了单项式除法以及代数式求值，正确掌握运算法则是解题关键．
练习册系列答案
相关题目
1．用一条长为60cm的绳子围成一个面积为acm2的长方形，a的值不可能为（ ）
| A． | 240 | B． | 225 | C． | 60 | D． | 30 |
2．
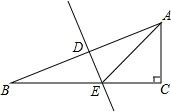在Rt△ABC中，斜边AB的垂直平分线DE，分别交AB、BC于D、E．
（1）若∠CAE=∠B+30°，求∠B的度数；
（2）若∠B=15°，AC=a，AB=b，求DE的长（用含a、b的代数式表示）．
在Rt△ABC中，斜边AB的垂直平分线DE，分别交AB、BC于D、E．（1）若∠CAE=∠B+30°，求∠B的度数；
（2）若∠B=15°，AC=a，AB=b，求DE的长（用含a、b的代数式表示）．
3．判断下列变量之间的关系是不是函数关系，是的画“√”，不是的画“×”，并在横线上写出理由．
（1）高线长h的等腰三角形的底边长a与面积S．（ ）√；
（2）关系式y=±$\sqrt{x}$中的y与x．（ ）×．
（3）下表中的v与s．（ ）√．
（4）关系式y=x2中的y与x．（ ）×．
（1）高线长h的等腰三角形的底边长a与面积S．（ ）√；
（2）关系式y=±$\sqrt{x}$中的y与x．（ ）×．
（3）下表中的v与s．（ ）√．
| 助跑速度v（m/s） | 7.5 | 8 | 8.5 |
| 跳远的距离s（m） | 4.78 | 5.44 | 6.14 |
如图所示，直线AB，CD相交于点O，OA平分∠EOC，若∠EOC=130°，则∠EOD=50°，∠AOD=115°．