题目内容
1.用配方法解下列方程:(1)x2-4x-5=0
(2)x2+6x+5=0.
分析 (1)常数项-5项后,应该在左右两边同时加上一次项系数-4的一半的平方,可得方程的解;
(2)把常数项5项后,应该在左右两边同时加上一次项系数6一半的平方,可得方程的解.
解答 解:(1)移项,得
x2-4x=5.
配方,得
(x-2)2=9,
开方,得
x-2=±3,
x1=5,x2=-1;
(2)移项,得
x2+6=-5.
配方,得
(x+32=4
开方,得
x-2=±2
x1=4x2=0.
点评 本题考查了配方法解一元二次方程,配方法的一般步骤:把常数项移到等号的右边;把二次项的系数化为1;等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
12.下列说法中,错误的是( )
| A. | 数轴上表示-5的点距离原点5个单位长度 | |
| B. | 规定了原点、正方向和长度单位的直线叫做数轴 | |
| C. | 有理数0在数轴上表示的点是原点 | |
| D. | 每一个有理数都能在数轴上找到一个点与它对应 |
6.将二次函数y=x2-2x+3化为y=a(x+h)2+k的形式,结果为( )
| A. | y=(x+1)2+2 | B. | y=(x-1)2+4 | C. | y=(x+1)2+4 | D. | y=(x-1)2+2 |
 已知G是△ABC的重心,AG=1,BG=3,CG=2$\sqrt{2}$,求S△ABC.
已知G是△ABC的重心,AG=1,BG=3,CG=2$\sqrt{2}$,求S△ABC.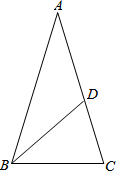 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC.